Точечная и пространственная симметрия

В физике твердого тела важную роль играет понятие геометрической симметрии. Симметрия означает возможность преобразования объекта, которое совмещает его с собой. Под симметрией кристаллов понимают свойство кристаллов совмещаться с собой после выполнения некоторых симметричных операций.

В общем значении симметрия – неизменность (инвариантность) объектов и законов при некоторых преобразованиях описывающих их переменных. Теория симметрии кристаллов – это теория симметричных преобразований самого в себя трехмерного пространства с учетом того, что внутренняя атомная структура кристаллов трехмерная периодическая, то есть описывается как кристаллическая решетка. Для кристаллов конечных размеров возможны такие операции симметрии как поворот кристалла на определенный угол и отображение в плоскости, для кристаллов бесконечных размеров следует прибавить еще трансляцию (параллельный перенос).

Операции симметрии – это отражения, вращения, переносы (трансляции), которые приводят пространство (фигуру) в совмещение с самим собой.

Для описания структуры конкретного кристалла необходимо:

– определить кристаллическую решетку;

– выбрать кристаллографическую систему координат;

– найти базис;

– определить набор преобразований симметрии, которая совмещает кристаллическую структуру саму с собой.

Элементы операций симметрии создают множество (конечное или бесконечное), которое называется группой симметрии. Множество элементов называется группой, если для этих элементов выполняются следующие условия:

1. На множестве элементов задан закон умножения элементов, то есть если элементы и 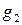принадлежат данному множест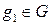ву ( , ), то их произведение также принадлежит множеству ( ).

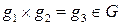2. На множестве элементов задан единичный элемент 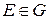такой, что выполняется .

3. На множестве элементов для каждого элемента имеется ему обратный 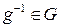, так что .

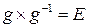4. Выполняется закон ассоциативности .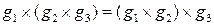

Бесконечный набор векторов трансляции, при переносе на которые кристалл совмещается сам с собой, образует трансляционную группу.

Кристаллические структуры имеют два типа симметричных преобразований: точечная симметрия и пространственная симметрия.

Точечной группой симметрии называют совокупность точечных операций симметрии, которые совмещают решетку саму с собой. Общее число независимых точечных групп симметрии кристаллов составляет 32. Эти группы включают конечное количество элементов.

Трансляционная симметрия отображает то обстоятельство, что одинаковые атомы в одинаковом окружении повторяются в разных точках кристалла и любую из этих точек можно перевести в положение, которое совпадает с другой точкой, с помощью операции трансляции.

Совокупность элементов точечной и трансляционной групп симметрии образуют пространственную группу симметрии. Общее количество независимых пространственных групп симметрии кристаллов 230.

Операции точечной симметрии оставляют неподвижной одну точку пространства. Представим список элементов точечной симметрии:

– плоскость симметрии (плоскость зеркальной симметрии);

– центр симметрии (центр инверсии);

– ось симметрии определенного порядка;

– инверсионные оси симметрии.

Плоскостью симметрии m (англ. mirror – зеркало) называется воображаемая плоскость, которая делит фигуру на две зеркально равные части.

Центром симметрии (инверсии) является особая точка, операция инверсии относительно которой приводит к идентичному взаимному расположению точек. Операция инверсии перемещает точку с координатами 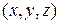в точку с координатами . Например, если мы посмотрим из центра элементарной ячейки с координатами [[1/2, 1/2, 1/2]], то в любом направлении картина будет такой же, как и в направлении 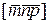. Понятно, что в решетке все узлы являются центрами симметрии решетки.

Осью симметрии порядка 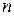называют воображаемую прямую, поворот кристалла вокруг которой на угол совмещает его с самим собой.

Операция зеркальной симметрии сводится к отображению в некоторой плоскости (зеркале), которую называют плоскостью симметрии.

Последовательно могут выполняться не только однотипные, но и разнотипные симметричные преобразования. Например, комбинация поворота вокруг оси и зеркальное отражение в плоскости, перпендикулярной к этой оси, приводит к появлению новых элементов симметрии – зеркально поворотных осей 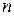-го порядка.

В кристаллах на элементы симметрии налагаются определенные ограничения. Можно доказать, что в кристаллах существуют только оси симметрии 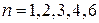-го порядков. Кристалл может быть симметричным относительно многих пересекающихся осей, но возможные угловые соотношения между осями жестко ограничены.

Оси пятого, седьмого и высших порядков в кристаллах невозможны, но они характерны для так называемых квазикристаллов и биологических объектов.

Сочетания последовательных вращений вокруг разных осей всегда связаны в группы из трех. Это случается потому, что поворот вокруг любой оси, например А, на угол со следующим поворотом вокруг оси В на угол 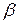может быть представлен единственным поворотом около некоторой третьей оси С на угол [1]. Каждому из возможных сочетаний осей симметрии отвечает кристаллографическая система (сингония) (см. табл.1.1 и табл.2.2).

В кристаллографии используется несколько способов обозначения элементов симметрии. Самыми распространенными являются международные обозначения, в которых поворотные оси отражаются цифрами 1, 2, 3, 4, 6; инверсионные – , зеркально поворотные – 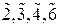. Плоскости симметрии помечают символом 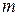. Записи × (точка), : (двоеточие), / (косая черта) означают, что плоскость соответственно является параллельной, перпендикулярной или наклоненная под углом к оси симметрии. Центр инверсии помечают .

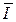Подобными международной символике являются обозначения Шубникова, в которых вместо зеркально инверсионных используются зеркально поворотные оси .

В физике твердого тела используются также обозначения Шенфлиса[2]:

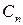– ось симметрии порядка ;

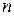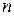– ось симметрии порядка и 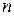осей, перпендикулярных к ней;

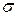– плоскость симметрии;

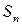– зеркально поворотная ось порядка ;

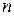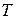– набор осей симметрии кубического тетраэдра;

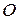– набор осей симметрии кубического октаэдра;

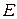– тождественное (единичное) превращение.

Индексами 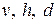около 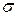отмечают соответственно вертикальную, горизонтальную и диагональную плоскости отражения. Вертикальная и диагональная плоскости проходят через вертикальную ось симметрии, горизонтальная – перпендикулярно к ней.