Подсчет и распределение угловой невязки
Суммируют измененные значения внутренних углов полигона и записывают это значение в ведомость (∑ 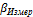 ).
).
Находят теоретическую сумму внутренних углов многоугольника по формуле
∑ 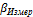 =180° (n-2),
=180° (n-2),
где n - число измеренных углов.
Определяют угловую невязку 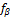 = ∑
= ∑ 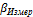 - ∑
- ∑ 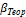
И записывают ее с соответствующим знаком в ведомость. Если бы результаты измерений не имели погрешностей, то угловая невязка равнялась бы нулю. Отсюда следует, что величина угловой невязки характеризует качество измерения углов. Предельно допустимую погрешность 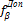 (невязку) угловых измерений вычисляют по формуле
(невязку) угловых измерений вычисляют по формуле
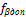 =±1'√n,
=±1'√n,
где n – число углов в ходе;
1'-предельная погрешность измерения одного угла теодолитом 4Т30П. Если выполняется условие 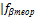 |≤|
|≤| 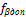 |, то точность полевых измерений углов считается удовлетворительной. В противном случае в результатах измерений или вычислениях имеется погрешность, которую надо обнаружить и устранить.
|, то точность полевых измерений углов считается удовлетворительной. В противном случае в результатах измерений или вычислениях имеется погрешность, которую надо обнаружить и устранить.
Результаты всех этих вычислений приводятся под итоговой чертой граф 2 и 3 в ведомости координат.
При упрощенном уравнивании углов полученную угловую невязку распределяют с обратным знаком во все измеренные углы. Поправка в каждый угол будет
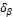 =
= 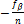
Если невязка не кратна числу углов, то большую поправку получают углы, составленные более короткими сторонами.
Для облегчения дальнейших вычислений возможно распределение поправок с целью округления десятых долей минут до целых минут. Поправки записывают красным цветом в графе 2 над минутами измеренного угла. Контролем увязки углов является выполнение условия
∑ 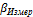 = ∑
= ∑ 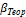 .
.
2. По исходному дирекционному углу сторон 1 – 2 (заданному преподавателем) и исправленным горизонтальным углам вычисляют дирекционные углы всех последующих сторон основного полигона по формуле
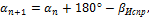
где αn=1- дирекционный угол последующей стороны;
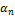 αn- дирекционный угол предыдущей стороны;
αn- дирекционный угол предыдущей стороны;
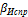 – увязанный (исправленный) горизонтальный угол, лежащий между предыдущей и последующей сторонами полигона.
– увязанный (исправленный) горизонтальный угол, лежащий между предыдущей и последующей сторонами полигона.
Вычисление дирекционных углов удобно производить на калькуляторах, при небольшом объеме работ вычисления можно выполнять на бумаге, располагая их в следующем порядке (вычисления приведены применительно к графе 4 табл.17):
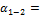 161°20'
161°20'
+180°00'
161°20'
- 119°51'
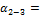 221°29'
221°29'
+180°00'
-105°48
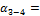 295°41'
295°41'
+180°00'
475°41'
- 100°29'
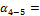 161°20'
161°20'
+180°00'
161°20'
- 119°51'
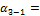 79°36'
79°36'
+180°00'
259°36'
- 98°16'
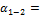 161°20'
161°20'
Если значение вычисленного дирекционного угла получилось больше 360°, то 360° надо вычесть. Вычисленные дирекционные углы выписываются в ведомость координат в графу 4.
Контролем правильности вычисления дирекционных углов в замкнутом полигоне является получение дирекционного угла исходной стороны 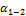 :
:
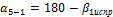 =
= 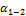 .
.
3. Получение дирекционные углы переводят в румбы. Зависимость между дирекционными углами и румбами представлена в табл. 15.
Таблица 15
Зависимость между дирекционными углами и румбами
| Четверть | Пределы значений дирекционных углов | Название румбов | Зависимость между дирекционными углами и румбами |
| І ІІ ІІІ ІV | 0° - 90° 90° -180° 180° -270° 270° -360° | СВ ЮВ ЮЗ СЗ | R = α R = 180°- α R = α - 180° R = 360° - α |
Проверить правильность определения румбов необходимо повторными вычислениями. Значения румбов выписывают в графу 5 ведомости координат.
4. По вычисленным значениям румбов и горизонтальным проложениям сторон (графы 5 и 6 ведомости координат) вычисляют приращения координат по формулам
∆ Х= ±d*cosr
∆ Y= ±d*sinr
где ∆ Х и ∆ Y – приращения координат соответственно по осям Х и Y;
D – горизонтальные проложения линий;
R – румбы линий.
Знаки приращений координат определяют по названиям румбов.
Таблица 16
Знаки приращений координат
| Названия румбов | ∆ Х | ∆ Y |
| СВ | + | + |
| ЮВ | - | + |
| ЮЗ | - | - |
| СЗ | + | - |
Вычисление приращений координат можно производить с помощью таблиц натуральных значений тригонометрических функций либо с помощью таблиц приращений координат, правила пользования которыми указаны в предисловии к ним.
Вычисленные значения приращений переписывают в соответствующие графы 7,8 ведомости координат с округлением до сотых долей метра.
Для грубого контроля следует запомнить, что при румбе линии до 45° ∆ Х >∆ Y, а при румбе лини больше 45° ∆ Х<∆ Y.
5. Вычисление линейной невязки замкнутого теодолитного хода, ее допуск и распределение.
Определяют невязки в приращении координат. Для этого находят алгебраическую сумму приращения координат отдельно по оси Х и по оси Y и подписывают ее внизу в столбцах 7,8 ∑ 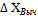 И ∑
И ∑ 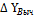 .
.
Вследствие неизбежных ошибок измерений, содержащихся в углах и сторонах хода, вычисленные суммы приращений, как правило, отличаются от теоретических. Их соответственные разности являются невязками по осям координат 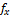 И
И 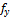 , т.е.
, т.е.
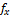 = ∑
= ∑ 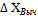 - ∑
- ∑ 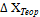
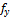 = ∑
= ∑ 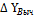 - ∑
- ∑ 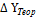
Известно, что в замкнутом ходе
∑ 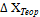 = 0; ∑
= 0; ∑ 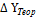 =0,
=0,
Откуда 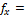 ∑
∑ 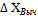 ;
; 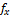 = ∑
= ∑ 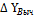 .
.
Определяют абсолютную невязку полигона
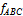 = ±
= ± 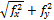
И относительную невязку
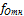 =
= 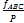 =
= 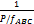 ,
,
где р – сумма горизонтальных проложений хода.
Относительная линейная невязка является показателем точности линейных измерений; допустимость ее определяется условиями измерений длин сторон полигона. Для благоприятных условий измерений величина относительной невязки не должна превышать 1:2000, для неблагоприятных – 1:1000, 1:1500. При допустимости относительной невязки в вычислительные значения приращений координат вводят поправки, которые записывают над соответствующими величинами X и Y. Поправки вычисляют, распределяя взятые с обратным знаком невязки 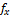 и
и 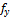 Пропорционально величинам соответствующим горизонтальных проложений (с округлением до сантиметра), по формулам
Пропорционально величинам соответствующим горизонтальных проложений (с округлением до сантиметра), по формулам
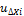 =
= 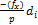 ;
; 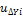 =
= 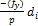 ;
;
где 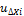 И
И 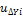 - поправки в приращениях координат соответственно по осям.
- поправки в приращениях координат соответственно по осям.
Так как величины невязок очень малы по сравнению с величиной периметра хода, то при прохождении ( 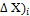 И
И 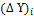
Периметры длины сторон округляют до десятков или сотен метров.
Например,
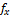 = +0,33;
= +0,33;
Р=7,3 сотни м;
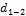 = 1,5 сотни м.
= 1,5 сотни м.
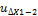 =
= 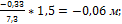
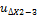 =
= 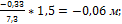
Суммы поправок в 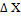 должны равняться «-»
должны равняться «-» 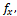 в
в 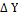 соответственно «-»
соответственно «-» 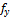 .
.
Суммируя алгебраически вычисленные значения приращений координат и поправок, получают исправленные значения 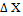 и
и 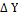 (столбцы 9,10). Контролем вычисления исправленных значений
(столбцы 9,10). Контролем вычисления исправленных значений 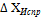 И
И 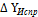 Является равенство их сумм нулю, т.е.
Является равенство их сумм нулю, т.е.
∑ 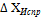 = 0; ∑
= 0; ∑ 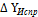 =0.
=0.
6. Вычисление координат X и Y точек полигона производится по формулам
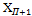 =
= 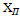 +
+ 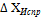
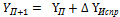
Исходными при этих вычислениях являются заданные преподавателем координаты т.1.
Контролем правильности вычисления координат являются получение координат исходной точки.
Дата добавления: 2016-07-11; просмотров: 22252;











