Види сигналів у системах з кодовим поділом сигналів
Як елементи складного сигналу найбільш часто використовуються:
− ортогональні сигнали (коди);
− псевдовипадкові послідовності.
Сигнал ортогональний на інтервалі 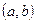 з вагою
з вагою 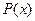 , якщо
, якщо
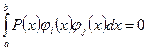 ,
, 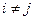 . (4.22)
. (4.22)
Такі сигнали описуються функціями Бесселя, багаточленами Чебишева тощо. Але точне їхнє відтворення дотепер не досягнуте.
Функції (коди) Уолша
Коди Уолша – одні з ортогональних кодів, які можна використовувати для кодування і подальшого об'єднання декількох інформаційних сигналів. Коди Уолша, як було показано в п. 4.1, формуються з рядків матриці:
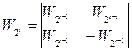 , (4.23)
, (4.23)
де 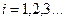
Особливість цієї матриці полягає в тому, що кожен її рядок ортогональний будь-якому іншому рядку.
При 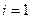
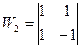 (часто записують у вигляді
(часто записують у вигляді 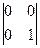 або
або 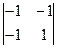 ).
).
Відповідно до цього співвідношення для 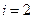
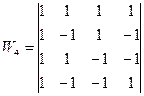 .
.
Набір функцій Уолша перших 8-ми порядків ( 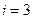 ) можна подати у вигляді матриці
) можна подати у вигляді матриці
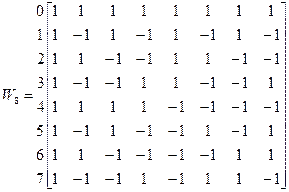 .
.
Характерно, що ВКФ 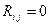 для всіх
для всіх 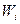 (за умовами відсутністі взаємного зсуву, тобто
(за умовами відсутністі взаємного зсуву, тобто 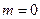 ). Наприклад, для
). Наприклад, для 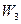 і
і 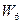 ,
, 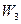
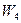 i
i 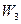 ,
, 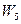 :
:

і так для інших пар з набору функцій Уолша.
Ортогональні коди Уолша широко використовуються у синхронних системах як каналоутворюючі, оскільки їхня взаємо-кореляційна функція дорівнює нулю, як розширювальні коди частіше використовуються псевдовипадкові послідовності (ПВП) різного виду.
Ортогональні коди мають два принципових недоліки:
– максимальна кількість можливих кодів обмежена їхньою довжиною, а відповідно, вони мають обмежений адресний простір.
– функція взаємної кореляції дорівнює нулю лише «у точці», тобто за відсутності часового зміщення між кодами. Тому такі сигнали використовуються лише в синхронних системах і переважно у прямих каналах (від базової станції до абонентської).
Псевдовипадкові послідовності
Поряд з ортогональними кодами ключову роль у CDMA-системах відіграють ПВП, які хоча і генеруються детермінованим чином, мають всі властивості випадкових сигналів. Однак вони вигідно відрізняються від ортогональних послідовностей інваріантістю до часового зсуву. Існує кілька видів ПВП, які мають різні характеристики. Вибір псевдовипадкової кодової послідовності в радіотехнічній системі передачі інформації дуже важливий, оскільки при одній і тій самій довжині кодової послідовності параметри (зокрема, завадостійкість) системи можуть бути різними.
ПВП мають відповідати таким критеріям, як непередбачуваність і випадковість. При генерації ПВП необхідно забезпечити відповідність властивостей цієї послідовності чітко певним критеріям випадковості:
1) збалансованість: кількість одиниць 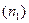 і кількість нулів
і кількість нулів 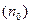 мають бути приблизно однаковими і рівними половині довжини ПВП
мають бути приблизно однаковими і рівними половині довжини ПВП 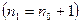 . Наприклад, у ПВП виду 000111101011001 загальна кількість розрядів
. Наприклад, у ПВП виду 000111101011001 загальна кількість розрядів 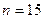 , з них кількість одиниць
, з них кількість одиниць 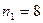 , кількість нулів
, кількість нулів 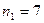 ;
;
2) серійність. Серією називається група з 0 або 1, що випливають підряд. Поява іншої цифри означає початок нової серії. Для ПВП характерно:
- довжина приблизно половини всіх серій дорівнює 1;
- довжина четвертої частини всіх серій – дорівнює 2 (групи з 2-х “1” або “0”);
- довжина 1/8 всіх серій – дорівнює 3 (групи з 3-х “1” або “0”);
- довжина 1/16 всіх серій – дорівнює 4 (групи з 4-х “1” або “0”) і т.д.
Наприклад, у ПВП виду 000111101011001 загальна кількість серій з одиниць і нулів дорівнює восьми (кожна з серій підкреслена): видно, що з восьми чотири серії довжиною в один розряд (0; 1; 0; 1), дві серії (четверта частина з усіх восьми) два розряди (11 і 00), одна серія (одна восьма з усіх) трьох розрядна (000) і одна серія довжиною в чотири розряди (1111).
3) властивість кореляції – при порозрядному порівнянні послідовностей, що зсуваються циклічно, різниця кількості збігів і кількості розбіжностей не повинна перевищувати 1, тобто модуль автокореляційної функції (АКФ) 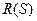 не повинен бути більше
не повинен бути більше 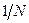 . Інакше кажучи, якщо значення розрядів ПВП (1 і 0) подані у вигляді +1 і −1 відповідно (що зазвичай має місце), то її автокореляційна функція
. Інакше кажучи, якщо значення розрядів ПВП (1 і 0) подані у вигляді +1 і −1 відповідно (що зазвичай має місце), то її автокореляційна функція 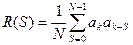 – періодична, причому її значення при
– періодична, причому її значення при 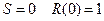 і при
і при 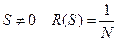 .
.
З числа псевдовипадкових послідовностей у системах з технологією CDMA широке застосування знаходять m-послідовності (МП), послідовності Голда, Касамі, широко використовуються функції (коди) Уолша, коди Баркера тощо.
М-послідовності
Одним з найбільш відомих фазоманіпульованих сигналів є сигнали, кодові послідовності яких мають максимальну довжину, є m-послідовності. Для m-послідовностей зазвичай використовують регістри зсуву або елементи затримки заданої довжини. Довжина m-послідовності дорівнює 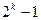 , де
, де 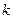 – число розрядів регістра зсуву. Різні варіанти підключення виходів розрядів до ланцюга зворотного зв'язку дають деякий набір послідовностей.
– число розрядів регістра зсуву. Різні варіанти підключення виходів розрядів до ланцюга зворотного зв'язку дають деякий набір послідовностей.
Розглянемо властивості МП (m-послідовностей) і способи їхнього формування.
1. Довжина МП (цикл, період МП) визначається співвідношенням 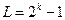 ,де k – ступінь полінома,
,де k – ступінь полінома, 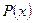 , на основі якого побудований формувач МП.
, на основі якого побудований формувач МП.
2. Верхня границя кількості різних МП визначається співвідношенням
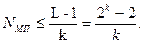 (4.24)
(4.24)
3. МП має властивість циклічності: порозрядна сума по 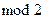 МП та її циклічно зсунутої копії являє собою теж МП, але з іншим циклічним зсувом.
МП та її циклічно зсунутої копії являє собою теж МП, але з іншим циклічним зсувом.
4. Будь-яка МП містить 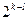 одиниць і
одиниць і 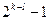 нулів (значення довжини МП – число непарне).
нулів (значення довжини МП – число непарне).
5. МП має раніше зазначену властивість випадковості – серійність.
6. Автокореляційна функція m-послідовності, у якій значення 1 і 0 замінені на +1 і -1 відповідно, є періодичною з періодом 2 k –1, а її значення визначається співвідношенням:
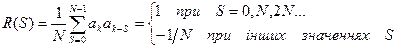 , (4.25)
, (4.25)
де 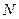 – розрядність
– розрядність 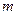 -послідовності (її довжина
-послідовності (її довжина 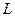 );
);
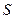 – значення взаємного часового зсуву двох копій
– значення взаємного часового зсуву двох копій 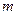 -послідовності на інтервал
-послідовності на інтервал 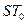 .
.
На рис. 4.7 наведений графік автокореляційної функції 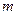 -послідовності для
-послідовності для 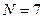 .
.

Рисунок 4.7 – Вид АКФ псевдовипадкової послідовності для 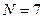 .
.
Властивість періодичності автокореляційної функції має важливе значення при використанні 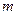 -послідовності для забезпечення циклової синхронізації. Крім того, два або більше незалежні сигнали можуть бути передані водночас в одній і тій самій смузі і потім успішно виділені, якщо вони являють собою циклічні зміщення m-послідовностей більш, ніж на один символ.
-послідовності для забезпечення циклової синхронізації. Крім того, два або більше незалежні сигнали можуть бути передані водночас в одній і тій самій смузі і потім успішно виділені, якщо вони являють собою циклічні зміщення m-послідовностей більш, ніж на один символ.
Для визначення структури цифрового автомата необхідно знати відповідний багаточлен 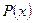 ступеня
ступеня 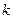 .
.
З усіх можливих багаточленів ступеня 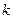 для синтезу цифрового автомата вибираються ті, що не розкладаються на співмножники. Крім того, багаточлен
для синтезу цифрового автомата вибираються ті, що не розкладаються на співмножники. Крім того, багаточлен 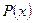 має бути примітивним (первісним), щодо двочлена
має бути примітивним (первісним), щодо двочлена 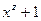 . Це означає, що двочлен
. Це означає, що двочлен 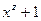 ділиться без залишку на
ділиться без залишку на 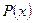 . Вибір такого багаточлена
. Вибір такого багаточлена 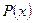 ступеня
ступеня 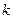 і побудова цифрового автомата (регістра зі зворотними зв'язками) відповідно до
і побудова цифрового автомата (регістра зі зворотними зв'язками) відповідно до 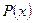 забезпечує формування ПВП з максимальним періодом
забезпечує формування ПВП з максимальним періодом 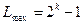 (тобто формування МП). Якщо обрано інший (не примітивні) багаточлен
(тобто формування МП). Якщо обрано інший (не примітивні) багаточлен 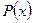 ступеня
ступеня 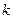 , то на його основі можна одержати ПВП з меншим періодом.
, то на його основі можна одержати ПВП з меншим періодом.
Щоб знайти період (цикл) ПВП L, необхідно біном 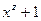 ділити на
ділити на 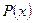 , змінюючи
, змінюючи 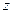 до величини, при якій розподіл здійснюється без залишку. Отримане значення
до величини, при якій розподіл здійснюється без залишку. Отримане значення 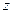 і визначає величину циклу L полінома
і визначає величину циклу L полінома 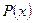 .
.
Для формування МП використовується регістр зсуву зі зворотними зв'язками за mod2. Функціональна схема формування МП (генератора, цифрового автомата) представлена на рис. 4.8.
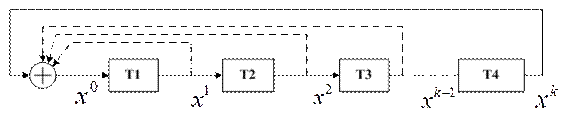
Рисунок 4.8 – Структурна схема цифрового автомата
Структура генератора m-послідовності визначається утворюючого багаточлена Р(х). У відповідності зі значенням ступеня полінома необхідно використовувати 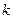 -розрядний регістр зсуву. Регістр має містити тригери
-розрядний регістр зсуву. Регістр має містити тригери 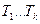 , з'єднані послідовно. Виходи тригерів, номери яких збігаються з ненульовими показниками ступеня членів полінома
, з'єднані послідовно. Виходи тригерів, номери яких збігаються з ненульовими показниками ступеня членів полінома 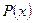 , з'єднуються з входами суматора по
, з'єднуються з входами суматора по 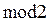 , а вихід суматора підключається до входу регістра. Як вихідний сигнал (МП) можна використовувати вихідний сигнал будь-якого осередку (тригера) регістра. Ці МП розрізняються лише величиною зсуву.
, а вихід суматора підключається до входу регістра. Як вихідний сигнал (МП) можна використовувати вихідний сигнал будь-якого осередку (тригера) регістра. Ці МП розрізняються лише величиною зсуву.
Під час використання технології множинного доступу з кодовим поділом каналів може виникнути необхідність виділення кожному абонентові «своєї» m-послідовності із числа можливих, кількість яких обмежена. Інакше кажучи, може з'явитися недолік m-послідовностей, що виявляється в обмеженості їхньої кількості. Від цього недоліку певною мерою вільні послідовності Голда, кількість яких значно перевищує кількість m-послідовностей, багато з яких мають добрі кореляційні властивості.
Послідовності Голда
Коди Голда з періодом 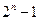 формуються на основі двох m-послідовностей з відбором так званих «кращих пар» (preferred pairs), що мають тризначну функцію автокореляції
формуються на основі двох m-послідовностей з відбором так званих «кращих пар» (preferred pairs), що мають тризначну функцію автокореляції 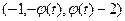 , де
, де
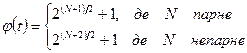 . (4.26)
. (4.26)
Коди Голда формуються шляхом посимвольного додавання за модулем 2 двох m-послідовностей (рис. 4.9).
Оскільки обидві МП, що використовуються для формування послідовності Голда, мають довжину 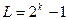 , та сформована послідовність Голда має таку саму довжину
, та сформована послідовність Голда має таку саму довжину 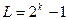 , але не є послідовністю максимальної довжини (
, але не є послідовністю максимальної довжини ( 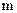 -послідовністю). Крім того, бажані послідовності Голда можна сформувати тільки за допомогою кращих пар m-послідовностей, структура яких визначається відповідними алгоритмами.
-послідовністю). Крім того, бажані послідовності Голда можна сформувати тільки за допомогою кращих пар m-послідовностей, структура яких визначається відповідними алгоритмами.
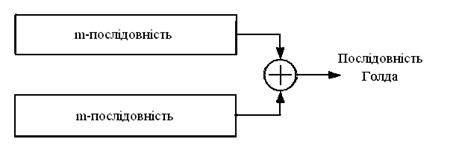
Рисунок 4.9– Генератор кодів Голда
Кількість різних послідовностей Голда, сформованих з двох МП, становить 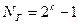 , оскільки при новому циклічному зміщенні початкових умов генераторів m-послідовностей формується нова послідовність Голда. Загальна кількість послідовностей з урахуванням використовуваних двох МП для формування послідовностей Голда становить
, оскільки при новому циклічному зміщенні початкових умов генераторів m-послідовностей формується нова послідовність Голда. Загальна кількість послідовностей з урахуванням використовуваних двох МП для формування послідовностей Голда становить
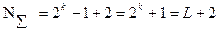 . (4.27)
. (4.27)
При виборі відповідної пари МП можна одержати сукупність послідовностей Голда з «добрими» кореляційними властивостями. Так, наприклад, при k=13 кількість МП дорівнює 630 і є пари таких МП, взаємна кореляційна функція яких R=703/L, тоді як серед послідовностей Голда можна вибрати пари з меншим значенням АКФ
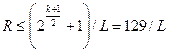 . (4.28)
. (4.28)
Послідовності Касами
Ще одним різновидом ПВП є послідовності Касами. Ці послідовності привабливі тим, що їх максимальна взаємна кореляційна функція для одного з варіантів послідовностей Касами (малий набір) становить 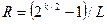 , а для іншого варіанта (великий набір послідовності Касами)
, а для іншого варіанта (великий набір послідовності Касами) 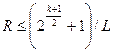 , де L – довжина послідовностей Касами, що дорівнює
, де L – довжина послідовностей Касами, що дорівнює 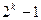 .
.
Послідовності Касами формуються для парних значень k. Принципи їхнього формування певною мірою аналогічні тим, які використовуються для послідовностей Голда з використанням процедур децимації вихідних m-послідовностей, комбінованої обробки послідовностей Голда і певних наборів уже сформованих послідовностей Касами. Сімейство кодів Касами містить 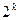 послідовностей з періодом
послідовностей з періодом 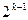 . Вони вважаються оптимальними в тому розумінні, що для будь-якої «кращої» пари забезпечується максимальне значення автокореляційної функції, що дорівнює
. Вони вважаються оптимальними в тому розумінні, що для будь-якої «кращої» пари забезпечується максимальне значення автокореляційної функції, що дорівнює 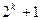 . Кодові послідовності Касами реалізуються за допомогою трьох послідовно включених регістрів зсуву (
. Кодові послідовності Касами реалізуються за допомогою трьох послідовно включених регістрів зсуву ( 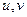 і
і 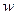 ) з різними зворотними зв'язками (рис. 4.10), кожний з яких формує свою
) з різними зворотними зв'язками (рис. 4.10), кожний з яких формує свою 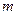 -послідовність.
-послідовність.
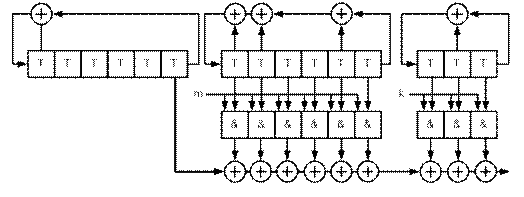
Рисунок 4.10 – Генератор послідовностей Касами типу kas(6, m, k),
де m і k – циклічні зміщення
Щоб одержати кодові послідовності Касами із заданими властивостями, послідовності v і w повинні мати різні зсуви.
Послідовності Баркера
Псевдовипадкові послідовності з малим значенням аперіодичної АКФ здатні забезпечити синхронізацію переданих і прийнятих сигналів за досить короткий проміжок часу, зазвичай дорівнює довжині самої послідовності. Найбільшу популярність одержали послідовності Баркера.
Кодова послідовність сигналу Баркера складається з символів +1 і -1. Його АКФ має вигляд
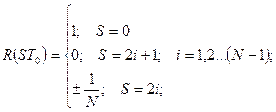 (4.29)
(4.29)

де 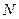 – число розрядів у сигналі Баркера. Знак в останньому рядку залежить від величини
– число розрядів у сигналі Баркера. Знак в останньому рядку залежить від величини 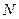 .
.
У табл. 4.1 наведені відомі коди Баркера для N=3,4,5,7,11,13. Для N>13 сигнали Баркера, які мають зазначену властивість АКФ не знайдені.
Таблиця 4.1 – Структура кодів Баркера
| Розрядність коду Баркера, N | Номери розрядів та їхні значення | ||||||||||||
| -1 | |||||||||||||
| -1 | |||||||||||||
| -1 | |||||||||||||
| -1 | -1 | -1 | |||||||||||
| -1 | -1 | -1 | -1 | -1 | -1 | ||||||||
| -1 | -1 | -1 | -1 | -1 |
Приклад, що пояснює вигляд АКФ сигналу Баркера для N=5, поданий на рис. 4.11.
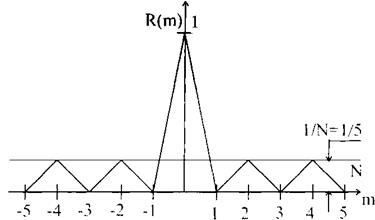
Рисунок 4.11 – Вид АКФ коду Баркера для N=5
На рис. 4.12 і 4.13 наведені схеми пристроїв формування і прийому сигналів Баркера для 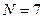 (структура сигналу 111-1-11-1) відповідно.
(структура сигналу 111-1-11-1) відповідно.
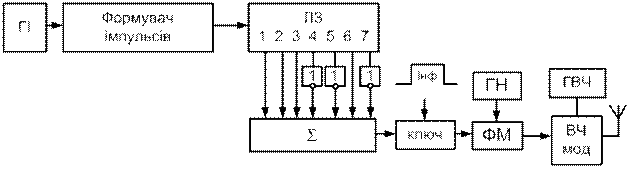 Рисунок 4.12 – Структурна схема формувача коду Баркера (N=7)
Рисунок 4.12 – Структурна схема формувача коду Баркера (N=7)
З виходу генератора імпульсів (ГІ) сигнали надходять на формувач, що формує імпульси необхідної форми й тривалості. Далі ці імпульси надходять на лінію затримки. З відводів лінії затримки сигнали подаються на суматор, а з його виходу сигнал Баркера надходить на модулятор.
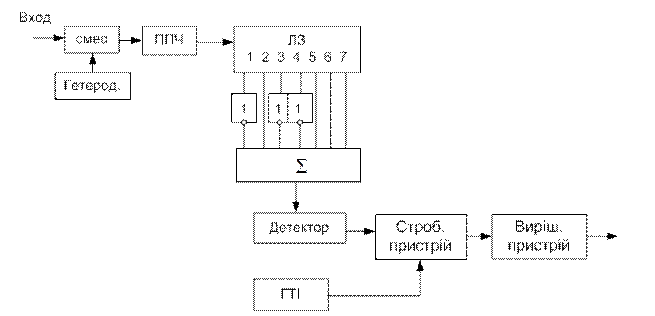
Рисунок 4.13 – Структурна схема приймача сигналів у коді Баркера ( 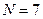 )
)
Прийом сигналів Баркера здійснюється пристроєм, що складається з вхідного фільтра і декодувального пристрою, що складається з суматора, лінії затримки і інверторів. Оскільки імпульсна характеристика фільтра збігається з IS-95 дзеркальним відбиттям сигналу, інвертори встановлені на виходах 1,3 і 4 лінії затримки.
Якщо сигнали Баркера передаються по кабелю, то немає необхідності в пристрої формування балансового модулятора і генератора ВЧ коливань.
Сигнали Баркера мають найкращі авто кореляційні властивості (АКФ). Тому їх найчастіше застосовують у якості синхросигналів для забезпечення циклової синхронізації.
Контрольні запитання та завдання
1. Коди Уолша використовуються для різних задач у прямому і зворотньому каналах. Поясніть використання кодів Уолша в обох випадках.
2. Дано 7 логічних каналів CDMA з кодами Уолша 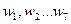 (
( 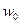 - не використовуються) у яких передаються інформаційні біти 1,0,0,1,1,0,1 відповідно до каналів
- не використовуються) у яких передаються інформаційні біти 1,0,0,1,1,0,1 відповідно до каналів 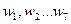 . Визначити структуру кодів Уолша. Визначити базу сигналу, сумарний сигнал, що передається: виділити з сумарного сигналу на приймальній стороні сигнал одного з каналів (1,2,3.4,5.6.7), вказаного викладачем.
. Визначити структуру кодів Уолша. Визначити базу сигналу, сумарний сигнал, що передається: виділити з сумарного сигналу на приймальній стороні сигнал одного з каналів (1,2,3.4,5.6.7), вказаного викладачем.
3. Визначити взаємнокореляційну функцію двох ПВП, сформованих за допомогою регістрів, побудованих на основі поліномів 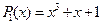 ,
, 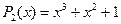 . Структуру ПВП знайти, використовуючи часову діаграму.
. Структуру ПВП знайти, використовуючи часову діаграму.
4. Визначити періодичну автокореляційну функцію ПВП, сформовану на основі полінома 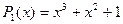 ,
, 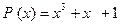 .Структуру ПВП знайти використовуючи часову діаграму роботи регістра.
.Структуру ПВП знайти використовуючи часову діаграму роботи регістра.
5. Загальне поняття про ШСС. Схема формування і прийому ШСС.
6. Геометричне і математичне уявлення ШСС.
7. Загальна методика синтезу системи складних сигналів.
8. М-послідовності. Їх властивості, схема, що реалізує МП.
9. Визначити кілкість можливих ШСС 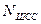 , якщо кількість часових інтервалів
, якщо кількість часових інтервалів 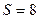 , кількість частотних інтервалів
, кількість частотних інтервалів 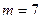 , кількість активних позицій
, кількість активних позицій 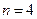 (код з постійною вагою «4 з 8»). Визначити кількість раціональних адрес.
(код з постійною вагою «4 з 8»). Визначити кількість раціональних адрес.
10. Наведіть геометричне подання часових, частотних і частотно-часових (Ч, ЧТ і ЧЧ) сигналів, що мають однакову базу 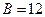 .
.
11.Наведіть варіант схеми формування і прийому ШСС, якщо інформаційні елементи «1» і «0» поданіі кодовими комбінаціями вигляду 100110 («1») і 110001 («0»).
12. Відношення сигнал/завада на вході приймача ШСС дорівнює -20 дБ. Визначити базу ШСС для забезпечення відношення сигнал/взаємна завада на виході приймача 10 дБ.
13. Визначити ймовірність помилки 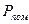 під час прийняття повідомлення, що повторюється 5 разів (
під час прийняття повідомлення, що повторюється 5 разів ( 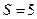 ) і приймається рішення за мажоритарною логікою "3 з 5". Ймовірність помилки при одноразовому прийомі повідомлення
) і приймається рішення за мажоритарною логікою "3 з 5". Ймовірність помилки при одноразовому прийомі повідомлення 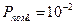 . Визначити і мінімізувати бульеву функцію, яка визначає структуру мажоритарного елементу "2 з 3".
. Визначити і мінімізувати бульеву функцію, яка визначає структуру мажоритарного елементу "2 з 3".
14. Закодувати 11 розрядну кодову комбінацію вигляду 1 0 0 1 1 1 0 1 0 1 1 манчестерським кодом. Визначити надмірність і швидкість передачі, якщо швидкість модуляції 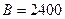 Бод.
Бод.
15. Кодові комбінації основного цифрового каналу ЦСП ( 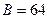 кБіт/с) перетворені в широкосмуговий сигнал з базою
кБіт/с) перетворені в широкосмуговий сигнал з базою 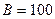 . Визначити швидкість передачі ШСС.
. Визначити швидкість передачі ШСС.
16. Розрахувати максимальне значення взаємно-кореляційної функції (ВКФ) 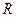 частотно-часових сигналів, якщо кількість часових інтервалів
частотно-часових сигналів, якщо кількість часових інтервалів 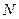 і хемінгова відстань коду
і хемінгова відстань коду 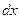 задані:
задані:
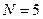 ,
, 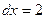 (1-й варіант);
(1-й варіант);
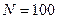 ,
, 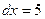 (2-й варіант);
(2-й варіант);
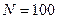 ,
, 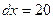 (3-й варіант).
(3-й варіант).
Порівняти і пояснити одержані результати.
17. Для формування М-послідовності використовується створюючий поліном 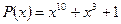 . Необхідно записати двійковий код поліному
. Необхідно записати двійковий код поліному 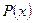 , визначити довжину циклу
, визначити довжину циклу 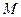 -послідовності, нарисувати схему цифрового автомата.
-послідовності, нарисувати схему цифрового автомата.
18. Заданий поліном 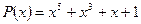 . Визначити цикл поліному
. Визначити цикл поліному 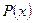 ; зобразити схему цифрового автомата, що формує
; зобразити схему цифрового автомата, що формує 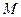 -послідовність.
-послідовність.
19. Схема цифрового автомата зображена на рис. 4.14. Визначити структуру створюючого полінома, його двійковий код, розрядність послідовності, що формується.
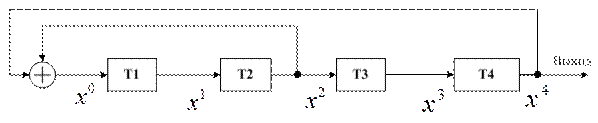
Рисунок 4.14 – Схема цифрового автомата.
20. Визначити АКФ коду Баркера для 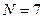 (його структура 111-1-11-l). Зобразити графік АКФ.
(його структура 111-1-11-l). Зобразити графік АКФ.
21. Зобразити схеми формування і прийому сигналів коду Баркера з 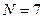 (його структура 111-1-11-1).
(його структура 111-1-11-1).
22. Визначити максимальну кількість абонентів, які можуть обслуговуватися, якщо значення бази 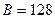 , допустиме відношення сигнал/взаємна завада (захищеність сигналу )
, допустиме відношення сигнал/взаємна завада (захищеність сигналу ) 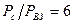 дБ, коефіцієнт
дБ, коефіцієнт 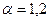 .
.
23. На рис. 4.15 зображена спрощена схема кодування і декодування CDMA сигналів, що надані. Використовується сім логічних каналів, у кожному з яких застосовується 7 бітовий код розширення. Всі джерела даних синхронізовані. Якщо всі сім джерел водночас передають один інформаційний біт у вигляді 7 розрядної послідовності імпульсів, на вхід приймача надходить комбінований сигнал. При збігу двох позитивних або негативних чисел сигнал посилюватиметься, два протилежні числа взаємно знищуватимуться. Для декодування даних певного каналу приймач умножує одержаний комбінований сигнал на відповідний цьому каналу код розширення, підсумовує одержані результати, після чого позитивному числу ставитися у відповідність двійковий символ 1, а негативному – двійковий символ 0.
Необхідно:
а) знайти коди розширення всіх каналів;
б) знайти вихідні сигнали всіх семи каналів;
в) знайти взаємну кореляцію каналу 1 і решти шести каналів, використовуючи знайдені значення кодів розширення.
На рис. 4.15 наведено вирішення задачі визначення вихідного сигналу першого каналу. Отримане позитивне число 9 вказує на те, що прийняте позитивне значення символу 1. Наведіть вирішення задачи усіх інших варіантів.
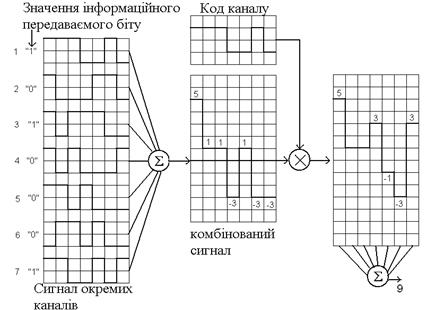
Рисунок 4.15 – Спрощена схема кодування і декодування СDMA сигналів
25. Доведіть, що коди Уолша матриці Адамара 8х8 взаємно ортогональні.
26. У системі CDMA користувачі А і В застосовують коди Уолша (-1 1 -1 1 -1 1 -1 1) і (-1 -1 1 1 -1 -1 1 1) відповідно. Необхідно визначити значення вихідного сигналу приймача якщо:
а) користувач А передає інформаційний символ (біт) 1, а користувач В не передає даних;
б) користувач А передає інформаційний символ (біт) 0, а користувач В не передає даних;
в) користувачі А і В водночас передають біти 1. Вважайте, що потужність сигналів, одержаних від А і В, однакова;
г) користувач А передає біт 0, а користувач В передає біт 1. Вважайте, що потужність сигналів, одержаних від А і В, однакова;
д) користувач А передає біт 1, а користувач В передає біт 0. Вважайте, що потужність сигналів, одержаних від А і В, однакова;
е) користувачі А і В водночас передають біти 0. Вважайте, що потужність сигналів, одержаних від А і В, однакова;
ж) користувачі А і В водночас передають біти 1. Вважайте, що потужність сигналу, одержаного від В, вдічі перевищує потужність сигналу А. Відміну потужності сигналів можна подати так: компоненти сигналу А записуються як (+1, -1), а компоненти сигналу В – як (+2, -2).
27. Наданий створюючий поліном для кодування циклічним кодом має вигляд 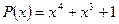 Необхідно:
Необхідно:
а) зобразити функціональну схему кодуючого пристрою;
б) закодувати послідовність бітів даних 10011011100;
в) припустивши, що один з бітів (будь-який) закодованої послідовності на вході приймача (декодера) спотворений, покажіть, що при декодуванні помилка буде знайдена.
28. Визначити втрати при розповсюдженні радіохвиль (в дБ) на відстані 25км від базової станції, що працює:
а) в частотному діапазоні 450МГц;
б) в частотному діапазоні 900МГц,
якщо висота антени базової станції 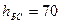 м, а висота антени мобільної станції
м, а висота антени мобільної станції 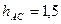 м. Передбачається робота у міському районі. Для визначення втрат необхідно використовувати модель Окамури-Хата.
м. Передбачається робота у міському районі. Для визначення втрат необхідно використовувати модель Окамури-Хата.
29. Поясніть різницю між видами модуляції BPSK і DQPSK.
30.Опишіть відмінності між методами багатостанційного (множинного) доступу частотного, часового і кодового доступу. Поясніть їх основні властивості.
31. Порівняйте схожість і відмінності в основних концепціях систем з прямим розширенням спектра і переналаштування робочої частоти.
32. Поясніть принцип наявності виграшу під час обробки сигналів у системах з розширенням спектра. Визначте поняття виграшу при обробці.
33. Які функції виконують псевдовипадкові послідовності у системах з CDMA?
34. Завада «ближній – дальній» являє серйозну проблему у стільникових системах з CDMA. Яка причина цього?
35. Адаптивне управління потужністю є рішенням проблеми «ближній – дальній» у системах CDMA. Опишіть два методи управління потужністю у системах CDMA.
Дата добавления: 2016-07-11; просмотров: 3991;











