Геометричне і математичне зображення широкосмугових сигналів

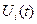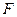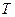У системах передачі дискретних сигналів кожному i-му повідомленню ставиться в однозначну відповідність сигнал з певної кінцевої безлічі сигналів. Для побудови цієї безлічі системі передачі виділяється смуга частот і час , обумовлений швидкістю передачі 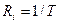. Отже, для формування сигналів на частотно-часовій площині виділяється область, що обмежена прямокутником зі сторонами 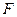і .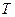

Для формування широкосмугових (складних) сигналів може використовуватися як вся область, так і її частина. Добуток 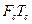є базою сигналу 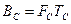, значення якої, 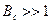. Іноді ШСС називають складними сигналами у відмінності від простих з базою сигналу, рівною одиниці, тобто .

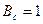В системах зв'язку зі ШСС ширина спектра 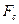завжди набагато більша ширини спектра початкового сигналу. Зазвичай, база ШСС досягає значень декількох сотень або навіть тисяч. Тому такі системи називають системами з розширеним спектром.

У загальному випадку складний сигнал можна подати у вигляді безлічі елементарних простих сигналів з тривалістю 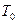кожний і зміщених за частотою на величину, кратну 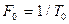(рис. 4.3).

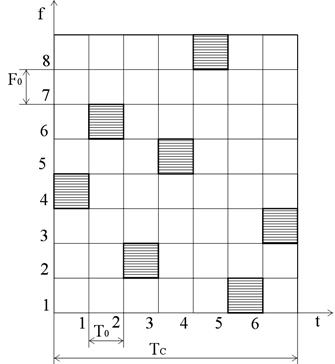
Рисунок 4.3 – Геометричне зображення ШСС

З рис. 4.3 видно, що інформаційний біт (розряд) розділений на 7 інтервалів тривалістю 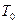кожний. Значення кожного з інтервалів (чіпів) передається на “своїй” частоті (на рис. 5.3 їхні значення : 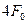; ; 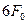; ; 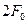; 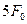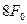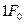і 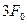відповідно).

Кожний з елементарних сигналів з амплітудою А, розташований в k-й часовій смузі і 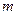-ю частотою 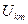, можна записати у вигляді

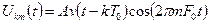, (4.3)

де

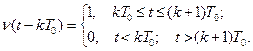
Співвідношення для складного сигналу, що складається з декількох елементарних, можна подати у вигляді:

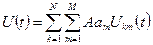, (4.4)

де 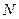і 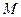– кількість часових і частотних інтервалів відповідно на частотно-часової площини (частотно-часової матриці).

Підставивши співвідношення для 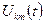у співвідношення для 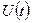одержимо:

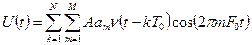. (4.5)

Зміна індексів 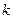і 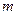означає зсув елементарного сигналу в часі на 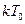і за частотою на 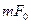. Наприклад,

.

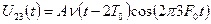За характером розподілу енергії на частотно-часовій площині сигнали розділяються на часові, частотні і частотно-часові.

Часові сигнали (сигнали з прямим розширенням спектра) не мають модуляції за частотою, тому 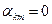для всіх 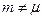. Тоді складний часовий сигнал (ЧС-сигнал) можна записати у такому вигляді:

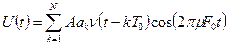. (4.6)

Умовний розподіл енергії ЧС-сигналу на частотно-часовій площині наведене на рис. 4.4.

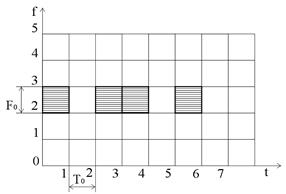
Рисунок 4.4 – Геометричне зображення складного часового сигналу

База кодування ЧС-сигналу

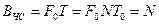. (4.7)

Частотні сигнали (сигнали зі стрибкоподібною перебудовою частоти) не мають модуляції в часі, тому 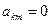для всіх .

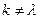Тоді складний частотний сигнал (Ч-сигнал) можна записати у вигляді:

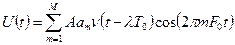. (4.8)

Умовний розподіл енергії Ч-сигналу на частотно-часовій площині наведено на рис. 4.5.

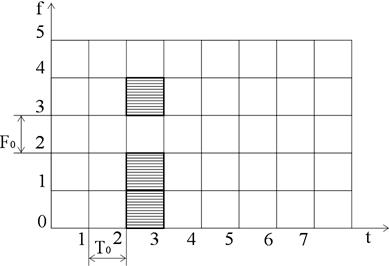
Рисунок 4.5 – Геометричне зображення складного частотного сигналу

База кодування складного Ч-сигналу

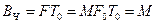. (4.9)

Частотно-часові сигнали (ЧЧ-сигнали зі стрибкоподібною перебудовою частоти) мають модуляцію як за частотою, так і у часі, тому співвідношення для складного ЧЧ-сигнала має вигляд

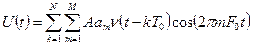. (4.10)

Геометрична інтерпретація цього сигналу являє собою частотно-часову матрицю (рис. 4.6).

База кодування ЧЧ-сигнала

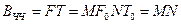. (4.11)

Тобто вона дорівнює загальній кількості елементів, з яких складається складний сигнал.

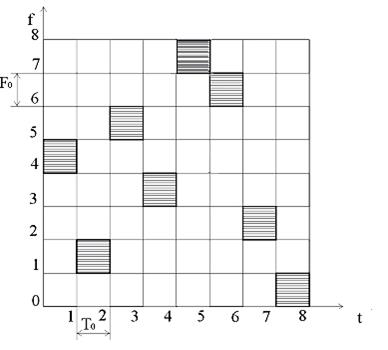
Рисунок 4.6 – Геометричне зображення складного частотно-часового сигналу

Порівняння систем складних сигналів необхідно проводити при однакових базах кодування і обсягах (кількості елементів) сигналів. Для забезпечення рівності баз сигналів 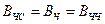необхідно для ЧС-сигналів збільшити 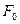в 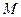разів, для Ч-сигналів збільшити 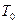у 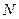разів. Ця умова приводить до того, що з усіх можливих сигналів вибираються лише ті, які мають однакову енергію. Наприклад, якщо складний сигнал має 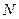часових інтервалів (розрядів), то для формування систем складних сигналів необхідно вибирати лише ті, які мають однакове число “1” і “0”.

Через те, що в широкосмугових системах (системах з кодовим поділом каналів) абоненти працюють одночасно у всій виділеній смузі частот, то виникають взаємні (структурні) завади. Рівень цих завад тим вище, чим більша кількість абонентів працює одночасно.

Найважливішою вимогою при виборі системи складних сигналів є однакова їхня завадостійкість при однаковій енергетиці. Для забезпечення однакової завадостійкості стосовно взаємних (структурних) завад необхідно, щоб адресні (абонентські) складні сигнали, які використовуються мали однакові взаємно кореляційні властивості.

Взаємно кореляційні властивості сигналів характеризуються взаємно кореляційною функцією (ВКФ) – 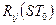. Безліч (сукупність) сигналів певного виду (структури) із ВКФ, що не перевершує за модулем деяке максимальне значення, тобто 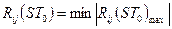, являє собою систему сигналів, а число сигналів, що відповідають зазначеній умові, називають обсягом системи сигналів.

Таким чином, система сигналів характеризується обсягом, ВКФ (R) і базою сигналу ( ).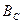

Для 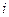-го і 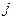-го сигналів ВКФ визначається співвідношенням

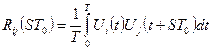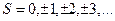, (4.12)

У порівнянні систем складних сигналів кращою з погляду завадостійкості стосовно структурних завад є та, котра забезпечує найменше з можливих максимальних значень ВКФ, тобто .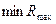

Співвідношення, що визначає ВКФ 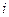-го і 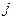-го частотно-часових сигналів у дискретних точках, має вигляд:

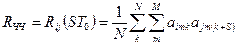, (4.13)

де .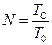

Для циклічного зсуву сигналу 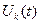на дискретний інтервал 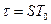необхідно визначати індекс 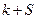за модулем цілого числа 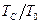. З наведеного співвідношення випливає, що значення 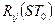пропорційне числу співпадаючих за частотою і за часом елементів i-го і циклічно зсунутого на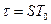 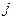-го сигналу:

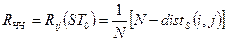, (4.14)

де 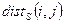– хемінгова відстань між 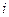-м і циклічно зміщеним на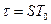 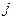-м сигналами (кількість незбіжних по частоті і за часом елементів цих сигналів). Відповідно до цього співвідношення максимум модуля ВКФ:

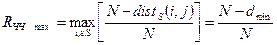, (4.15)

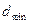– кодова відстань обраного часового коду;

де 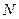– число часових інтервалів (розрядів).

З аналізу співвідношення для 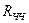випливає, що, по-перше, при збільшенні надмірності (при збільшенні кодової відстані 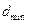) при незмінному числі часових інтервалів 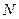величина ВКФ ( 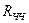) зменшується. Зі збільшенням же 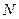при незмінній величині 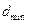величина ВКФ зростає. По-друге, аналіз показує, що синтез складних ЧЧ-сигналів зводиться до побудови кодів, інваріантних до циклічного зсуву. Системі ЧЧ-сигналів відповідає код, що зберігає мінімальну кодову відстань при будь-яких циклічних зсувах.

Співвідношення для ВКФ часових сигналів (ШСС з прямим розширенням спектра) має вигляд:

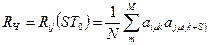. (4.16)

При амплітудній модуляції (АМ) елементів ШСС коефіцієнти 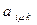і 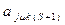приймають значення 0 або 1.

У цьому випадку ВКФ і максимум її модуля визначаються тими самими співвідношеннями, що і для ЧЧ-сигналів:

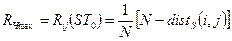. (4.17)

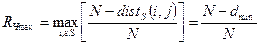. (4.18)

Системою часових АМ-сигналів є код, що зберігає мінімальну кодову відстань 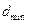за будь-яких циклічних зміщеннь.

При фазовій модуляції елементів ШСС коефіцієнти 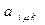і 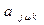приймають значення 1 або -1. Тоді зі співвідношення для ВКФ Ч-сигналів випливає, що 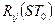пропорційна різниця між кількістю співпадаючих і елементів, що розрізняються по фазі елементів 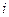-го і циклічно зсунутого 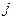-го сигналів:

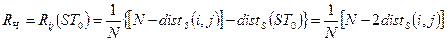, (4.19)

де 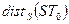– кількість елементів, що розрізняються за фазою, 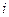-го і на 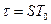циклічно зсунутого 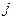-го сигналів (хемміногова відстань між цими сигналами). При цьому максимум модуля ВКФ:

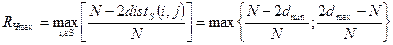, (4.20)

де 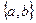– найбільша з величин a і b.

Значення цих величин передбачається позитивними, тому що в коді, як правило, , .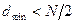

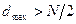Таким чином, системою Ч-сигналів є код, що зберігає за будь-яких циклічних зсувів як максимальну, так і мінімальну кодову відстань.

Для частотних (Ч) сигналів співвідношення для ВКФ має вигляд:

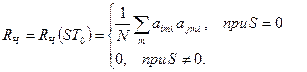. (4.21)

Звідси випливає, що ВКФ дорівнює нулю при всіх часових інтервалах, крім нульового, між i-м і j-м сигналами. Максимальне значення ВКФ досягається тільки в точці 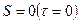. Тому властивість кодів зберігати мінімальну або максимальну кодову відстань за будь-яких циклічних зсувів тут не потрібна. Для системи Ч-сигналів може бути використаний будь-який код.

Методика побудови системи складних сигналів полягає в наступному.

1. Необхідно вибрати метод модуляції, що визначає вид сигналу (ЧС, Ч або ЧЧ).

2. При заданій кількості абонентів 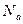і наявної сукупності сигналів 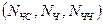необхідно вибрати 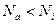складних сигналів і визначити для кожної пари сигналів ВКФ.

3. Вибрати ті сигнали для системи складних сигналів, які задовольняють умові .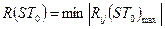

Можна зробити висновок про те, що для одержання виграшу якості зв'язку під час використання кожного зі способів кореляційної обробки, необхідно, щоб ансамбль сигналів мав «добрі» автокореляційні властивості. Бажано, щоб сигнали мали єдиний автокореляційний пік, інакше можлива помилкова синхронізація за бічним пелюстком автокореляційної функції (АКФ). Важливо, що чим ширше спектр випромінюваних сигналів, тим більш вузький центральний пік (основний пелюсток) АКФ. Пари кодових послідовностей підбираються так, щоб взаємна кореляційна функція (ВКФ) мала мінімальне значення при їхній попарній кореляції. Це гарантує мінімальний рівень взаємних завад.

Отже, вибір оптимального ансамблю сигналів в CDMA зводиться до пошуку такої структури кодових послідовностей, у якій центральний пік АКФ має найбільший рівень, а бічні пелюстки АКФ і максимальні викиди ВКФ за можливості мінімальні.