Загальна характеристика широкосмугових сигналів

Використання широкосмугових сигналів дозволяє радіостанціям працювати одночасно і в одній і тій самій смузі частот. Передані сигнали усіх абонентів (АС) розрізняються за формою, що і дозволяє розділити їх у приймачах. Кожен приймач із усієї безлічі прийнятих сигналів виділяє "свої" сигнали, форма яких відома у приймачі і відрізняється від форми сигналів усіх інших абонентів. Як такі сигнали, що розрізняються за формою, використовують широкосмугові сигнали (ШСС).

ШСС – це такі сигнали, у яких добуток ширини спектра сигналу Р_с на його тривалість 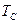набагато більше одиниці, тобто 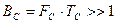. Цей добуток називається базою сигналу 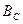. Іноді ШСС називають складними сигналами на відміну від простих з базою сигналу, рівною одиниці, тобто .

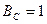На основі ШСС будуються системи множинного доступу з СDMA.

У системах зв'язку з ШСС ширина спектра F_с завжди набагато більше ширини спектра вихідного сигналу. Тому в сучасній технічній літературі такі системи називають системами з розширеним спектром. У системах зв'язку з ШСС елементам дискретних сигналів надають складну форму (структуру).

Один з можливих варіантів схеми формування і прийому ШСС із використанням погодженого фільтра наведений на рис. 4.1.

Лінія затримки (ЛЗ) має 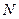відводів, встановлених через рівні інтервали з затримкою кожного з них на час 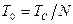. Частина відводів приєднується до cхеми суматора 1, частина – до суматора 2. На вхід ЛЗ із періодом T_C безперервно подаються короткі (тактові) імпульси. Ключ (модулятор) встановлюється в те або інше положення залежно від переданих інформаційних одиничних елементів (“1” або “0”), що мають бути передані. Внаслідок цього на виході модулятора видаються послідовності імпульсів, кожна з яких однозначно пов'язана з переданим інформаційним одиничними елементом (“1” або “0”). Цими послідовностями імпульсів модулюється передавач ВЧ коливань (ВЧ ПД).

Дешифрація прийнятих ШСС здійснюється за допомогою ЛЗ (погодженого фільтра), інтеграторів і тригера. Настроївши дешифратор на виділення “своїх” кодових комбінацій (послідовностей імпульсів), якими закодовані інформаційні “1” і “0”, можна забезпечити прийом сигналів, адресованих даному абоненту.

Зазвичай, база ШСС досягає значень від 10 до декількох тисяч.

У розглянутій схемі інформаційні символи “1” і “0” кодуються кодовими комбінаціями різної структури, якими модулюється генератор ВЧ.

Іншим варіантом передачі сигналів є варіант, при якому адреси абонентів кодуються різними послідовностями імпульсів, а зміст переданих одиничних елементів “1” або “0” укладено у фазі сигналу.

Очевидно, що завадостійкість системи зв’язку з кодовим поділом сигналів стосовно взаємних завад тим вище, чим менше взаємний зв’язок між сигналами (адресами) абонентів, тобто чим менше їх взаємно кореляційна функція (ВКФ). Тому при побудові таких систем необхідно вирішувати завдання побудови систем складних сигналів, що забезпечують у приймачах абонентів найменший рівень структурних завад.

Рисунок 4.1 – Схеми формування і прийому ШСС

Кодове ущільнення (поділ) сигналів широко використовується в різних радіосистемах, особливо у системах рухомого радіозв’язку.

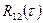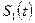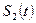Можливість кодового ущільнення (ущільнення сигналів за формою заснована на кореляційних властивостях широкосмугових сигналів. Взаємно кореляційною функція (ВКФ) сигналів і , що мають кінцеві енергіїї, є функція, що визначається співвідношенням:

, (4.1)

де 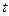– час; – величина зсуву в часі другого сигналу щодо першого.

Фізичний зміст ВКФ є ступінь подоби двох сигналів. Окремим випадком ВКФ є автокореляційна функція (АКФ), коли 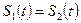. Чим більше схожі сигнали один на одного, тим більше позитивне значення має ВКФ. Якщо значення функції 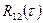має найбільше абсолютне значення і негативний знак, то це вказує на те, що сигнали і 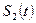протилежні, тобто 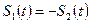. Для кодового поділу каналів, застосованого у стандартах CDMA, важливий випадок, коли 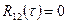у точці, або 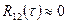на всьому відрізку визначення зсуву τ. Сигнали, що задовольняють першій рівності, називаються ортогональними "у точці", сигнали, що задовольняють другій приблизній рівності – квазіортогональними. Сигнали, для яких ВКФ чітко дорівнює нулю при всіх часових зсувах, не існують, тому, говорячи про ортогональні коди, мається на увазі ортогональність "у точці ". У зв'язку із зазначеними випадками розглядають два типи адресних систем з кодовим ущільненням сигналів: синхронні та асинхронні. Прикладом систем із кодовим ущільненням сигналів є синхронні адресні системи, які використовуються у системі стандарту IS-95.

Сутність кодового ущільнення сигналів від базової станції (БС) до абонентської (АС), зводиться до наступного:

- N інформаційним потокам, призначеним для 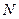абонентів, привласнюється своя кодова псевдовипадкова послідовність (ПВП);

- кодові послідовності некорельовані між собою;

- бінарні інформаційні потоки модулюються власними ПВП;

- канальні широкосмугові сигнали складаються в підсумовуючому пристрої;

- модуляція несучої складним широкосмуговим сигналом і випромінювання радіосигналу у простір.

Спрощена схема формування групового сигналу, що реалізує викладені принципи, зображена на рис. 4.2.

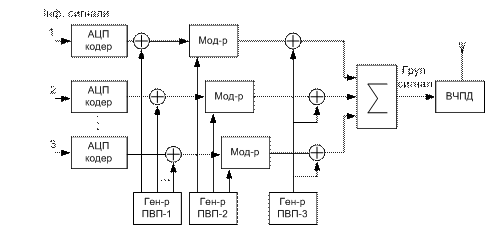
Рисунок 4.2 – Схема формування групового сигналу

На приймальній стороні в абонентській станції:

- відома "своя" кодова послідовність;

- здійснюється перенесення сигналу з радіочастоти в область низьких частот;

- низькочастотний імпульсний сигнал надходить на вхід корелятора, на другий вхід якого синхронно надходить кодуюча ПВП;

- корелятор, що складається з перемножника та інтегратора, обчислює взаємнокореляційну функцію двох сигналів;

- відгук на виході корелятора відбувається тільки тоді, коли в ущільненому складному сигналі присутня "своя" ПВП, у протилежному випадку на виході спостерігається тільки шум.

Нині відомо чимало методів формування ансамблів ортогональних і квазіортогональних послідовностей. Серед ортогональних систем сигналів у ряді систем зв'язку для кодового поділу застосовуються сигнали, що є рядками матриці Адамара розміром 64×64. Матриця Адамара розміром 2n×2n формується з матриці розміром n×n у такий спосіб:

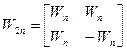. (4.2)

Початковою матрицею в цьому рекурентному обчисленні виступає матриця розміром 1х1: W1 = [1]. Таким чином, матриця Адамара розміром 2х2

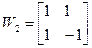
За аналогією матриця 8х8 має вигляд:

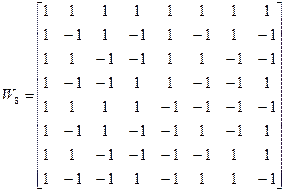
Можна переконатися, що якщо попарно перемножити елементи двох різних рядків матриці, а потім скласти результати, то вийде нуль. Це означає, що будь-яка пара рядків у матриці Адамара є ортогональною (зрозуміло, якщо немає взаємного зсуву). З іншого боку, кореляція рядка самого собою дає число 8, що очевидно. Якщо ж скорелювати рядок з його інверсним поданням, то результат дорівнюватиме – 8. Таким чином, інформаційний "0" першого каналу можна передавати першим рядком матриці Адамара, а інформаційну "1" – першим рядком, але з інверсією; бінарному потоку другого каналу можна привласнити другий рядок і т.д. Оскільки рядки матриці ортогональні, то сигнали різних каналів можна розділити на приймальній стороні. Рядки матриці Адамара частіше називаються функціями Уолша.

Системи зв'язку, що базуються на кодовому поділі каналів порівнянно з іншими системами цифрового зв'язку, мають суттєві переваги:

- мають виняткову складність результуючих сигналів, тим самим підвищуючи конфіденційність передачі;

- мають малу спектральну щільність результуючого сигналу, що підвищує скритність системи;

- ефективно передають інформацію при багатопроменевому поширенні радіохвиль;

- стійкі до впливу як імпульсних, так і зосереджених за частотою завад;

- здійснюють близьку до когерентного обробку сигналів, тим самим доводячи завадостійкість до граничних значень;

- мають низький рівень споживаної потужності абонентської станції, що забезпечує її тривалу роботу без підзарядки;

- полегшують або повністю виключають необхідність частотного планування;

- гнучкі в розгортанні, легко адаптуються до вимог за наданими послугами у конкретній мережі користування.

Висока ефективність використання частотного ресурсу, висока завадозахищеність, скритність і конфіденційність привели до того, що сучасні системи, зокрема, мобільного зв'язку, орієнтовані на ті або інші варіанти CDMA.