Метод Зейделя-Гаусса
В отличие от метода простой итерации метод Зейделя-Гаусса отличается тем, что получаемые значения переменных сразу вступают в расчетный процесс:
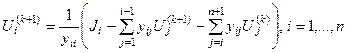 .
.
В матричном виде такой процедуре соответствует запись:
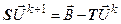
где 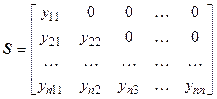 ,
, 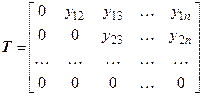 ,
,
а рекуррентное выражение представляется в виде:
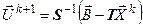 .
.
Сходимость метода Зейделя-Гаусса, как правило, лучше, но может быть и хуже, чем в простой итерации. Это зависит от характеристик матрицы коэффициентов.
Пример: Для рассмотренной в предыдущем примере электрической сети методом Зейделя-Гаусса решить систему уравнений узловых напряжений.
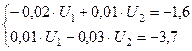
Рекуррентное выражение для метода Зейделя-Гаусса:
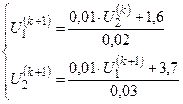 .
.
Первое уравнение как в методе простой итерации. Второе отличается подстановкой вместо 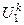 значения
значения 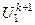 .
.
Для организации итерационного процесса возьмем начальное приближение напряжений, равное напряжению балансирующего узла: 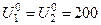 .
.
Итерация 1.
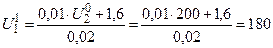
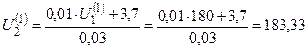
Точное решение этим методом достигается за семь итераций, т.е. почти в два раза быстрее, чем методом простой итерации.
Дата добавления: 2020-07-18; просмотров: 676;











