Итерационные методы решения систем линейных и нелинейных уравнений
Итерационными называются методы, позволяющие получить последовательность приближений переменных к решению: 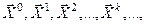 где k– номер итерации (приближения),
где k– номер итерации (приближения), 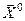 - некоторое начальное приближение.
- некоторое начальное приближение.
Каждое следующее k+1 приближение получается из предыдущего, с помощью единообразных вычислений по так называемому рекуррентному выражению 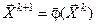 - для одношаговых и
- для одношаговых и 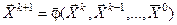 - для многошаговых методов.
- для многошаговых методов.
Если предел последовательности 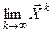 существует, то итерационный процесс называется сходящимся. В этом случае
существует, то итерационный процесс называется сходящимся. В этом случае 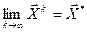 , где
, где 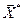 - решение системы
- решение системы 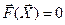 . В противном случае итерационный процесс является расходящимся и получить решение рассматриваемым методом не представляется возможным.
. В противном случае итерационный процесс является расходящимся и получить решение рассматриваемым методом не представляется возможным.
Для ограничения итерационного процесса принимаются те или иные критерии. Наиболее распространенными среди них являются ограничение по сходимости 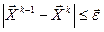 (
( 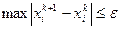 ), ограничение по значению функции
), ограничение по значению функции 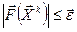 (
( 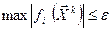 ), где
), где 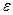 - приемлемая для данной задачи достаточно малая величина. Возможна комбинация критериев или иные интегральные условия, например
- приемлемая для данной задачи достаточно малая величина. Возможна комбинация критериев или иные интегральные условия, например 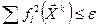 и др.
и др.
Итерационные методы различаются в зависимости от вида рекуррентного выражения.
Дата добавления: 2020-07-18; просмотров: 662;











