Общий вид формул преобразования коэффициентов
Введем обозначения : i - номер уравнения (строки); j - номер переменной (элемента в строке); к - номер шага преобразования (исключаемой переменной)
Тогда формулы преобразования расписываются так:
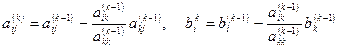 . .
| (3.8) |
Эти формулы легко поддаются программированию для использования вычислительной техники.
Общий вид формул обратного хода
На каждом следующем шаге k (k=n-1,...,1) вычисляется значение переменной xk
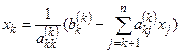 .
.
Блок-схема метода Гаусса
1. Ввод исходных данных.
Прямой ход
2. Цикл по исключаемым переменным k =1,…,n-1.
3. Цикл по уравнениям i=2,…,n.
4. c= 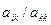 .
.
5. Цикл по текущим переменным j=i,…,n.
6. 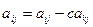 .
.
7. Next j; Next i ; Next k
Обратный ход
8. xn= bn/ann.
9. Цикл по восстанавливаемым переменным k =n-1,…, 1.
10. Цикл по текущим переменным j=k+1,…,n, S=0.
11. S=S+ 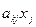 ; Next j.
; Next j.
12. 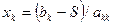 ; Next k
; Next k
Пример. Методом Гаусса решить систему линейных уравнений
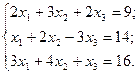
Из первого уравнения системы выразим значение переменной 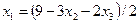 и подставим его во второе и третье уравнения
и подставим его во второе и третье уравнения
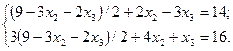
После приведения подобных членов последние уравнения имеют вид
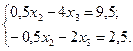
Аналогично из второго уравнения выразим значение переменной 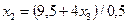 и подставим его в третье уравнение
и подставим его в третье уравнение 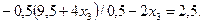
В результате система уравнений преобразуется к треугольному виду
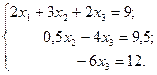
Это прямой ход исключения Гаусса. На обратном ходе значения переменных определяются в обратном порядке (снизу вверх). Из третьего уравнения 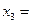 -2. Из второго после подстановки
-2. Из второго после подстановки 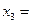 -2 получаем х2=3 и из первого х1=2.
-2 получаем х2=3 и из первого х1=2.
Процедуру прямого хода можно представить в матричной форме. Исключение переменных осуществляется путем вычитания предварительно умноженной на коэффициент ki строки, соответствующей исключаемой переменной, из нижних строк
| Исходная Расширенная матрица | Матрица после первого исключения | Матрица после второго исключения |
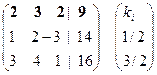
| 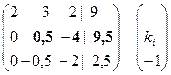
| 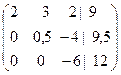
|
Дата добавления: 2020-07-18; просмотров: 957;











