Алгоритм триангуляции

Основная идея метода Гаусса широко используется в различных алгоритмических модификациях. Выбор алгоритма решения СЛУ в электроэнергетике должен учитывать следующие особенности уравнений, описывающих установившиеся режимы энергосистемы:

При анализе режимов ЭЭС рассматриваются изменяющиеся во времени нагрузки узлов для сетей постоянной конфигурации, где матрица проводимостей Y остается неизменной. Изменяется только правая часть СЛУ (токи, мощности). Следовательно, требуется выбрать такой алгоритм, который в максимальной степени учитывает специфику постоянства матрицы проводимостей.

Анализ (3.8) позволяет видеть, что при повторных расчетах, связанных с изменением правой части СЛУ выполняются одни и те же преобразования матрицы коэффициентов { 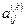}. На этапе исключения переменных новые величины { 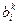} составляют примерно 2/n часть. Было бы желательно сохранить промежуточные расчеты { 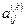} для их последующего использования.

Это оказывается возможным благодаря так называемой процедуре триангуляции, согласно которой матрица коэффициентов представляется в виде произведения двух треугольных матриц A=LW, причем одна из них (L) является треугольной «снизу», а другая (W) – треугольной «сверху». Представление A=LW называется треугольным разложением или триангуляцией матрицы.

Решение системы линейных уравнений с триангулированной матрицей коэффициентов сводится к двум решениям систем уравнений с треугольными матрицами. Предположим, что требуется решить систему уравнений:

,

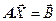(4.1)

причем

A =LW.

Заменив в (4.1) A на LW,получаем

.

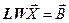Обозначим 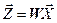, тогда вместо системы(4.1) можно записать две эквивалентные:

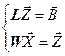
(4.2)

Из первого матричного уравнения решением СЛУ с треугольной матрицей Lопределяется вектор 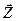, а из второй – искомый вектор 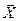. При однократном решении СЛУ триангуляция не дает каких-либо преимуществ по сравнению с простым методом Гаусса. Однако при каждом последующем изменении вектора 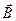расчеты СЛУ производятся по (4.2) с неизменными матрицами L,W. При этом решение занимает гораздо меньше времени, чем решение системы с исходной матрицей А, поскольку исключаются повторные расчеты { 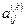} (они сохранены в матрицах L, W).

Рассмотрим триангуляцию квадратной матрицы, т.е. разложение её на треугольные сомножители.

Прежде всего, проанализируем формулу (3.8) преобразования коэффициентов в прямом ходе метода Гаусса:

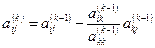
По существу, данная формула означает вычитание на шаге k (исключение переменной x_k) умноженной на коэффициент 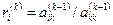строки k (управляющая строка -УСТР) из текущей строки i. Коэффициенты 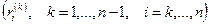используются при формировании матрицы L. Совокупность 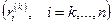обычно называется управляющим столбцом (УСТБ).

Следует отметить, что любое преобразование матрицы (например, вычитание из какой-либо строки другой, умноженной на некоторый коэффициент) означает ее умножение на некоторую, совершенно определенную матрицу, или иначе, если в результате преобразования матрицы А получена матрица W, то можно записать А=LW.

В приведенном ниже примере матрица Wполучена из А вычитанием первой строки из второй, а матрица Lполучена по некоторому, известному нам правилу.

.

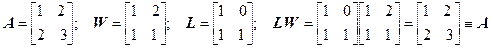Таким образом, в примере показано, что действительно, существует матрица L, характеризующая линейные преобразования исходной матрицы.

Можно показать, что матрица Lформируется последовательно из управляющих столбцов в процессе гауссовского исключения переменных. Один шаг эквивалентен преобразованию с матрицей, построенной из единичной заменой k-го столбца управляющим столбцом. В частности, на первом шаге А=L₁W₁, на второмW₁=L₂W₂, на n-1W _n-2=L_n-1W _n-1=L_n-1W. Отсюда А=LW, где результирующая матрица определяется произведением L =L₁L₂…L_n-1 и представляет собой совокупность управляющих столбцов_.

, ,…,

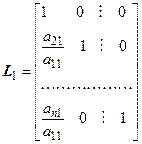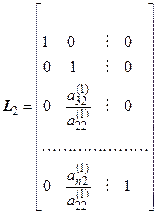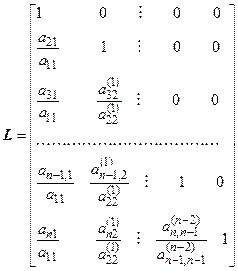
Матрица Wявляется результатом процесса исключения переменных или последовательно формируется из управляющих строк

; ;

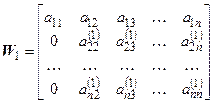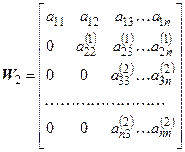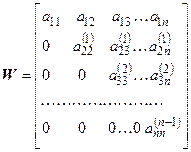
Свойство симметричности матрицы проводимостей ( 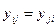) позволяет отказаться от формирования и хранения матрицы L, поскольку управляющие столбцы легко получаются из управляющих строк

,

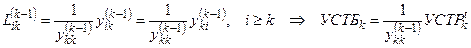т.е. столбец k матрицы L равен транспонированной строке k матрицыW, деленной на ее диагональный элемент.