Свойства обратной матрицы
1. Определитель обратной матрицы отличен от нуля. Произведение определителей исходной и обратной матрицы равно единице, Det(А)·Det(А-1)= 1.
2. Матрица, обратная по отношению к А-1, совпадает с исходной, (А-1)-1 = А
3. Обратная матрица единственна, т.е. если для матрицы А различными методами найдены матрицы В1 и В2, обладающие свойствами обратной, то В1 = В2
4. Обратная матрица может быть вычислена через матрицу алгебраических дополнений Δ
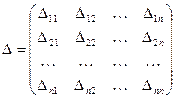 , соответствующую
, соответствующую 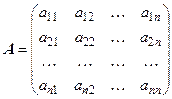
согласно выражению 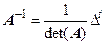 .
.
Отсюда для получения обратной матрицы методом алгебраических дополнений (один из возможных методов) можно сформулировать следующий алгоритм.
a) Вычислить определитель, 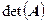 .
.
b) Сформировать матрицу, каждый элемент которой есть алгебраическое дополнение соответствующего элемента исходной матрицы: 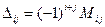 .
.
c) Транспонировать матрицу алгебраических дополнений.
d) Каждый элемент транспонированной матрицы умножить на коэффициент 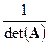 .
.
Пример. Исходная матрица 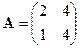 . Найти обратную матрицу
. Найти обратную матрицу 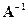 по приведенному правилу и доказать, что она обратная.
по приведенному правилу и доказать, что она обратная.
Решение:
Определитель исходной матрицы 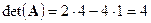 ,
,
Матрица алгебраических дополнений Δ= 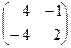
Транспонированная матрица алгебраических дополнений Δt= 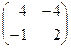 ,
,
Обратная матрица 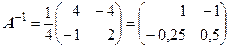 .
.
Проверка(при ручных расчетах рекомендуется делать всегда, как только будет получена обратная матрица).
Если 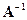 — обратная, то справедливо выражение
— обратная, то справедливо выражение 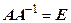 .
.
A 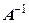 =
= 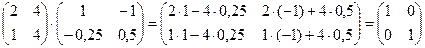 .
.
Получена единичная матрица, следовательно, расчет выполнен правильно
Дата добавления: 2020-07-18; просмотров: 570;











