Решение для переменного значения коэффициента диффузии.
В реальных экспериментах величина коэффициента диффузии 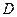 не является константой. Даже для одного и того же состава он может меняться в зависимости от времени, если меняется температура. Коэффициент диффузии может также зависеть от состава, а, следовательно, при наличии градиента концентрации, меняться от точки к точке по объёму образца.
не является константой. Даже для одного и того же состава он может меняться в зависимости от времени, если меняется температура. Коэффициент диффузии может также зависеть от состава, а, следовательно, при наличии градиента концентрации, меняться от точки к точке по объёму образца.
В случае, если коэффициент диффузии 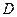 есть функция времени, а не координат, то второе уравнение Фика можно записать как
есть функция времени, а не координат, то второе уравнение Фика можно записать как
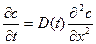 .
.
Это значит, что можно использовать все решения, применявшиеся для постоянного значения коэффициента диффузии, при этом заменив 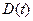 его средним значением
его средним значением
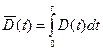 . (1.68)
. (1.68)
Это значение берётся обычно в диффузионных расчетах при введение поправок на нагрев до температуры отжига и последующего охлаждения или при использовании сложного цикла отжигов.
Рассмотрим одномерную задачу, в которой коэффициент диффузии есть функция координаты, т.е. 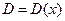 . Второе уравнение Фика в этом случае имеет вид:
. Второе уравнение Фика в этом случае имеет вид:
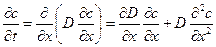 . (1.69)
. (1.69)
Член 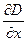 делает решение этого уравнения неоднородным, и получить его в замкнутом виде трудно, либо невозможно.
делает решение этого уравнения неоднородным, и получить его в замкнутом виде трудно, либо невозможно.
Предположим, что причиной диффузии является градиент концентрации 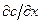 . В этом случае зависимость от координаты
. В этом случае зависимость от координаты 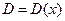 однозначно связана с зависимостью от концентрации. Рассмотрим решение для
однозначно связана с зависимостью от концентрации. Рассмотрим решение для 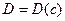 .
.
Можно начальное условие записать через одну переменную 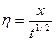 при этом
при этом 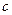 есть функция только
есть функция только 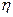 . В этом случае уравнение (1.69) перейдёт в обычное однородное дифференциальное. Используя переменный параметр
. В этом случае уравнение (1.69) перейдёт в обычное однородное дифференциальное. Используя переменный параметр 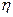 , получим:
, получим:
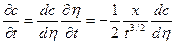
и
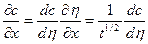 .
.
Подставляя последние выражения в уравнение (1.69), получим:
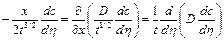
или
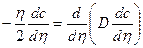 . (1.70)
. (1.70)
Переход от уравнения (1.69) к (1.70) сделал Больцман. Для определения 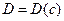 Матано рассмотрел полубесконечную диффузионную пару (см. раздел 1.4.2.3.), которая описывается следующими начальными условиями:
Матано рассмотрел полубесконечную диффузионную пару (см. раздел 1.4.2.3.), которая описывается следующими начальными условиями:
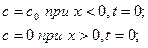
Так как точка 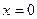 исключена из рассмотрения при
исключена из рассмотрения при 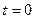 и исходная концентрация не зависит от расстояния, то, отбросить разрыв при
и исходная концентрация не зависит от расстояния, то, отбросить разрыв при 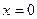 , начальное условие можно записать только через
, начальное условие можно записать только через 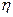 :
:
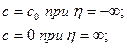
Уравнение (1.70) содержит только полные дифференциалы, поэтому можно его сократить на 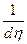 слева и справа и проинтегрировать от
слева и справа и проинтегрировать от 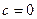 до
до 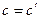 , где
, где 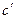 - любая концентрация
- любая концентрация 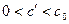
Возвращаясь к прежним переменным можно записать
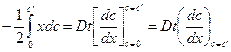 . (1.71)
. (1.71)
Последнее равенство в выражении (1.71) следует из того в бесконечной системе, 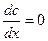 как при
как при 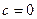 , так и при
, так и при 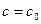 . Следовательно,
. Следовательно,
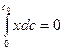 . (1.72)
. (1.72)
Это условие определяет плоскость, на которой 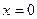 . Имеется в виду плоскость, разделяющая вещества
. Имеется в виду плоскость, разделяющая вещества 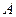 и
и 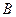 (см. рис.1.1.) при
(см. рис.1.1.) при 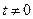 .
.
При таком условии, зависимость коэффициента диффузии от концентрации можно получить графическим интегрированием и дифференцированием 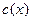 с помощью соотношения
с помощью соотношения
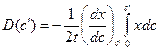 . (1.73)
. (1.73)
Экспериментальные данные по диффузии из одного вещества ( 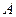 ) в другое
) в другое 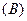 можно представить графически, как показано на рисунке на рисунке 1.4. Точка
можно представить графически, как показано на рисунке на рисунке 1.4. Точка 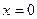 (штриховая линия на рисунке) определяется в соответствии с уравнением (1.72) и называется поверхностью Матано. Эта линия, которая делит заштрихованную область на две равные по площади половины.
(штриховая линия на рисунке) определяется в соответствии с уравнением (1.72) и называется поверхностью Матано. Эта линия, которая делит заштрихованную область на две равные по площади половины.
Величину 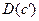 для выбранного
для выбранного 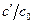 рассчитывают по измеренной площади участка, заштрихованного в клетку (интеграл
рассчитывают по измеренной площади участка, заштрихованного в клетку (интеграл 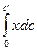 ), и обратной величине наклона касательной к кривой (производной
), и обратной величине наклона касательной к кривой (производной 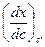 ) в этой точке. Этот метод получил название метода Больцмана – Матано.
) в этой точке. Этот метод получил название метода Больцмана – Матано.
Ошибки в вычислениях 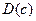 велики при
велики при 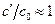 и
и 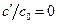 , так как в окрестности этих точек площадь очень мала, а производная
, так как в окрестности этих точек площадь очень мала, а производная 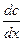 очень велика. Для уменьшения ошибки кривую зависимости концентрации от расстояния обычно строят по точкам методом наименьших квадратов – в результате она должна быть похожа на кривую, представленную на рис. 1.4.
очень велика. Для уменьшения ошибки кривую зависимости концентрации от расстояния обычно строят по точкам методом наименьших квадратов – в результате она должна быть похожа на кривую, представленную на рис. 1.4.
|
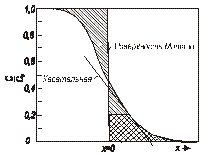
Рисунок 1.4. Поверхность Матано расположена так, чтобы заштрихованные участки слева и справа от нее были равны. Площадь, заштрихованная в клетку, и касательная – величины, используемые для расчета 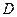 при при 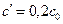 . .
|
Эффект Киркендалла
При расчете коэффициента диффузии в методе Больцмана – Матано по сути определяется коэффициент взаимной диффузии 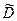 , который описывает процесс гомогенизации сплава. Это ставит новую задачу определения связи между
, который описывает процесс гомогенизации сплава. Это ставит новую задачу определения связи между 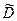 и коэффициентами самодиффузии компонентов
и коэффициентами самодиффузии компонентов 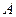 и
и 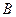 при том же составе сплава.
при том же составе сплава.
На первый взгляд, кажется, что 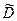 является средним значением коэффициентов диффузии двух компонентов. Однако, если оба компонента диффундируют с различными скоростями, то необходимо ввести дополнительный параметр, определяющий эту разницу. Впервые этот параметр экспериментально определил Киркендалл. Он намотал на прямоугольный пруток латуни (сплав меди с цинком) молибденовую тонкую проволоку и затем нанёс на этот образец слой чистой меди. (рис. 1.5). Молибден практически нерастворим ни в меди, ни в латуни и поэтому никакого участия в диффузии не принимает. Таким образом, был изготовлен образец с неравновесной концентрацией цинка и начальными условиями, соответствующими системе пары полубесконечных тел.
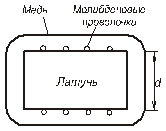
является средним значением коэффициентов диффузии двух компонентов. Однако, если оба компонента диффундируют с различными скоростями, то необходимо ввести дополнительный параметр, определяющий эту разницу. Впервые этот параметр экспериментально определил Киркендалл. Он намотал на прямоугольный пруток латуни (сплав меди с цинком) молибденовую тонкую проволоку и затем нанёс на этот образец слой чистой меди. (рис. 1.5). Молибден практически нерастворим ни в меди, ни в латуни и поэтому никакого участия в диффузии не принимает. Таким образом, был изготовлен образец с неравновесной концентрацией цинка и начальными условиями, соответствующими системе пары полубесконечных тел.
|
| Рис.1.5. Сечение диффузионной пары в эксперименте Киркендалла. |
Образец был подвергнут серии последовательных отжигов, в результате которых цинк диффундировал из латуни в медь, а медь из внешней зоны диффундировала в латунь. После каждого отжига от образца отрезался кусок и измеряли расстояние между витками молибдена ( 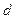 ). Было установлено, что
). Было установлено, что 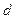 монотонно убывает со временем. Поскольку общий объём образца не менялся, то такая кинетика возможна в случае, если поток цинка превосходит поток меди через одну и ту же плоскость. Сдвиг молибденовых меток в латунь направлен в сторону, противоположную диффузионному потоку цинка.
монотонно убывает со временем. Поскольку общий объём образца не менялся, то такая кинетика возможна в случае, если поток цинка превосходит поток меди через одну и ту же плоскость. Сдвиг молибденовых меток в латунь направлен в сторону, противоположную диффузионному потоку цинка.
Каков механизм движение меток? Даркен показывает это на следующем простом примере. Всем известна диффузия чернил в воде. Под диффузионным движением понимается движение молекул или атомов. Представим ту же ситуацию когда чернила вылиты в реку, у которой имеется собственное движение – течение. Тогда для наблюдателя на берегу скорость движения чернил является результатом сложения скорости потока воды и скорости диффузии чернил. Чтобы измерить скорость диффузионного потока необходимо выбрать систему отсчёта, связанную с водой реки и тем самым исключить роль течения. Даркен предлагает связать эту новую систему отсчёта с щепкой, плывущей по течению. В случае нашей задачей роль щепки играют молибденовые метки, которые дрейфуют (текут) вместе с кристаллической решёткой - аналогом реки. Их положение определяет истинную поверхность раздела системы медь - латунь
Диффузионные потоки компонентов 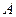 и
и 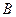 в системе отсчёта, связанной с метками, не равны
в системе отсчёта, связанной с метками, не равны 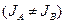 . Но в неподвижной системе отсчёта, связанной, например, с внешней поверхностью образца (берегом реки) потоки компонентов
. Но в неподвижной системе отсчёта, связанной, например, с внешней поверхностью образца (берегом реки) потоки компонентов 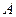 и
и 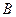 (
( 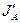 и
и 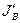 ) выравниваются за счёт течения решётки
) выравниваются за счёт течения решётки 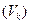 .
.
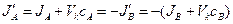 , (1.74)
, (1.74)
где 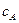 и
и 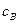 - концентрации компонентов, рассчитываемые как число атомов на единицу объёма.
- концентрации компонентов, рассчитываемые как число атомов на единицу объёма.
В такой постановке задачи потокам 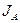 и
и 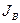 соответствуют собственные коэффициенты диффузии
соответствуют собственные коэффициенты диффузии 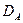 и
и 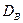 , а потокам
, а потокам 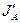 и
и 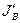 коэффициент взаимной диффузии
коэффициент взаимной диффузии 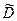 .
.
Воспользовавшись первым уравнением Фика запись (1.74) можно представить как
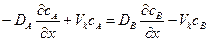 (1.75)
(1.75)
При постановке этой задачи было оговорено, что объём системы в процессе отжига не меняется. Следовательно, общее число атомов в единице объёма 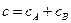 есть величина постоянная, а
есть величина постоянная, а 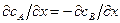 . Заменив концентрацию молярными долями компонентов:
. Заменив концентрацию молярными долями компонентов: 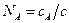 и
и 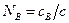 , получим из уравнения (1.75) выражение для скорости течения решётки.
, получим из уравнения (1.75) выражение для скорости течения решётки.
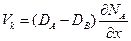 (1.76)
(1.76)
Следовательно, скорость течения решётки и соответственно дрейфа молибденовых меток определяется разницей собственных коэффициентов диффузии.
Для установления связи между 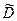 и собственными коэффициентами диффузии подставим уравнение (1.75) в уравнение (1.74)
и собственными коэффициентами диффузии подставим уравнение (1.75) в уравнение (1.74)
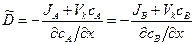 (1.77)
(1.77)
Учитывая вывод (1.76) выражение для коэффициента взаимной диффузии приобретает вид
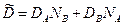 (1.78)
(1.78)
Полученные формулы полностью описывают результаты для изотермического отжига в бесконечном образце. По сути просто утверждается, что если происходит движение меток, то величины 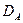 и
и 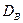 различны и их можно определить для заданного состава путем измерения
различны и их можно определить для заданного состава путем измерения 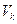 и
и 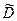 . В разбавленном растворе
. В разбавленном растворе 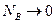 и
и 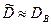 , т.е. коэффициент взаимной диффузии определяется скоростью диффузии атомов примеси. Если
, т.е. коэффициент взаимной диффузии определяется скоростью диффузии атомов примеси. Если 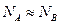 , но
, но 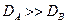 коэффициент взаимной диффузии
коэффициент взаимной диффузии 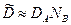 , т.е. скорость перемешивания определяется диффузией более быстрого компонента.
, т.е. скорость перемешивания определяется диффузией более быстрого компонента.
В рассматриваемой системе медь – латунь Смигельскас и Киркендалл установили, что расстояние между молибденовыми метками (находящимися на поверхности раздела системы медь – латунь) растёт пропорционально корню квадратному из времени.
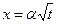 (1.79)
(1.79)
Тогда скорость дрейфа меток
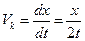 (1.80)
(1.80)
При рассмотрении метода Больцмана – Матано (раздел 1.7) было введено понятие поверхности Матано (уравнение 1.72), как границы раздела диффузионной пары, изменяющей своё пространственное положение по мере увеличения времени отжига. Выражениями (1.79) и (1.80) по сути и определяется её положение и скорость перемещения, т.е. метки всегда находятся на поверхности Матано. Основным свойством этой поверхности является постоянство концентрации диффундирующего вещества на неё для всех 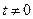 . В эксперименте Смигельскаса и Киркендалла концентрация цинка на этой поверхности соответствовала содержанию 22,5%
. В эксперименте Смигельскаса и Киркендалла концентрация цинка на этой поверхности соответствовала содержанию 22,5% 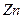 . Они нашли, что за 56 дней при температуре равной 785оС метки сдвинулись на 0,0125 см. Для этого состава Даркен получил следующие коэффициенты собственной диффузии:
. Они нашли, что за 56 дней при температуре равной 785оС метки сдвинулись на 0,0125 см. Для этого состава Даркен получил следующие коэффициенты собственной диффузии:
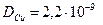 см2/сек;
см2/сек;
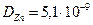 см2/сек;
см2/сек;
В твердых растворах замещения собственные коэффициенты диффузии обычно отличаются менее чем на порядок. Когда это различие становится больше, скорость дрейфа меток сильно возрастает (например, системы 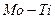 ,
, 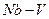 ) и опытные значения
) и опытные значения 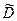 становятся такими, что для их объяснения одному из собственных коэффициентов диффузии приписывается отрицательное значение, что не имеет физического смысла.
становятся такими, что для их объяснения одному из собственных коэффициентов диффузии приписывается отрицательное значение, что не имеет физического смысла.
Бардин и Херринг объясняют сдвиг молибденовых меток возникновением в зоне взаимной диффузии вакансионного потока ( 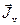 ), компенсирующего разность потоков компонент:
), компенсирующего разность потоков компонент:
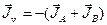
Этот поток направлен в строну более быстрого компонента. В нашем случае в сторону потока 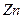 , т.е. в латунь.
, т.е. в латунь.
Со стороны меди возникает избыток вакансий по сравнению с их термодинамически равновесной концентрацией, что приводит к образованию вакансионных пор. Лишние вакансии должны исчезнуть в диффузионной зоне, например, поглотиться дислокациями за счёт их переползания. При таком движении дислокаций число узлов кристаллической решётки в единице объёма сохраняется, однако, переползание приводит к исчезновению атомных экстраплоскостей. Если до начала диффузии ( 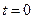 ) метки находились в плоскости раздела диффузионной пары, созданной экспериментатором (т.н. плоскость Киркендалла), то в процессе отжига они сместятся в сторону цинка, оставаясь теперь всё время на поверхности Матано (
) метки находились в плоскости раздела диффузионной пары, созданной экспериментатором (т.н. плоскость Киркендалла), то в процессе отжига они сместятся в сторону цинка, оставаясь теперь всё время на поверхности Матано ( 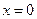 ).
).
Таким образом, теория Бардина – Херринга в место течения решётки создаёт механизм вакансионного дрейфа меток. Их сдвиг есть следствие стремления системы установить равновесную концентрацию вакансий.
Проведенные ими расчёты показали, что скорость смещения плоскости Киркендалла ( 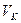 )можно выразить как
)можно выразить как
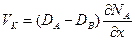 , (1.81)
, (1.81)
что совпадает с уравнением (1.76) для скорости течения решётки. Поэтому сдвиг меток за счёт течения решётки или потока вакансий физически идентичны.
2 АТОМНАЯ ТЕОРИЯ ДИФФУЗИИ
Дата добавления: 2020-07-18; просмотров: 1008;











