Утворення дефектів при загартуванні.
На практиці зустрічаються такі випадки, коли концентрації точкових дефектів виявляються на багато порядків вище відповідних рівноважних значень. Однак подібні ситуації у твердих тілах можуть виникати, якщо тверде тіло піддавалося якимсь додатковим спеціальним зовнішнім впливам. Причин, що можуть приводити до підвищення концентрації точкових дефектів, досить багато. Розглянемо деякі з них.
При підвищенні температури кристалу термодинамічно рівноважні концентрації вакансій зростають. Якщо нагрітий кристал різко охолодити, то високотемпературну концентрацію точкових дефектів можна «заморозити», так що при низькій температурі їх концентрація виявиться вище рівноважної. Очевидно, що загартування може бути ефективним лише за умови, що швидкість загартування більше швидкості встановлення в системі термодинамічної рівноваги, що визначається дифузійною рухливістю дефектів при цій температурі. Гартівна процедура дає можливість експериментально визначити багато характеристик точкових дефектів: енергію утворення, міграційну енергію й ін. Проте, в умовах великих концентрацій дефектів можливо їхнє зіткнення, наслідком чого може бути утворення зв'язаних дефектів або комплексів, наприклад дивакансій, що можуть мігрувати навіть швидше, ніж одиничні точкові дефекти. У деяких випадках формуються більш стабільні скупчення точкових дефектів – кластери або дислокаційні петлі.
Точкові дефекти в металах існуютьпри всіх температурах більших за нуль, проте їх число мале при кімнатній температурі (Т=20 0С). Для того, що би вивчати особливості поведінки дефектів і їх вплив на властивості кристалів, потрібно одержати їх якомога в більшій нерівноважній концентрації. Відомі три методи отримання нерівноважної концентрації: загартування, пластична деформація, опромінення частинками високих енергій. Розглянемо одержання високих концентрацій дефектів методом загартування.
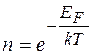 . (3.1.1)
. (3.1.1)
Як слідує із (3.1.1) n швидко зростає при збільшенні Т.
Рівноважна концентрація точкових дефектів досягається і підтримується за рахунок того, що дефекти дифундують до внутрішніх і зовнішніх поверхонь і від них. Дефекти будучи дуже швидкими при високих температурах, неперервно виникають і зникають на цих поверхнях і як наслідок їх концентрація підтримується за рахунок динамічної рівноваги. При даній Т швидкість встановлення нової рівноважної концентрації дефектів визначається середньою віддалю між джерелами і стоками, а також енергією активації переміщення і температурою Т. Рівновага завжди встановлюється швидше при підвищенні Т, чим при її зменшенні, так як рухливість дефектів експоненційно наростає із збільшенням Т. В процесі загартування зразок приводять в рівноважний стан при високій Т, яка називається температурою загартування Тq і потім охолоджують до низької ТL настільки швидко, щоб зберіглась концентрація дефектів.
При виборі Tq та ТL слід враховувати ряд обставин. Величина ТL повинна бути настільки мала, щоб не зменшувалась n при проведені вимірів. Із одержаних раніше оцінок слідує, що по мірі підвищення Т зростає доля дефектів, які об’єднуються в комплекси. Якщо потрібно одержати тільки ізольовані дефекти, то це об’єднання визначає верхню границю для температури Тq, в той же час нижня границя обумовлена мінімальною кількістю дефектів, яка необхідна для вимірів.
В якості простого прикладу розглянемо об’єднання дефектів при високій температурі в золоті [Келлер]. Цим автором розраховано рівноважну концентрацію моновакансій V1 і дивакансій V2 при різних температурах загартування із співвідношень 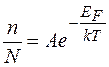 і
і 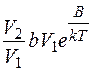 , в передекспоненційні множники яких введені значення, що відповідають приблизній оцінці зміни ентропії . Для золота отримано
, в передекспоненційні множники яких введені значення, що відповідають приблизній оцінці зміни ентропії . Для золота отримано
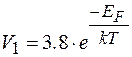 та
та 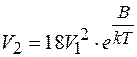 . (3.1.2)
. (3.1.2)
При EF=0.98еВ В = 0.1; 0.2; 0.3.
Таблиця 3.1. Рівноважні концентрації моно- і дивакансій в Cu
| Т°,C | V1 | B=0.3еВ | 0.2eB | 0.1eB | |||
| V2 | V2/V1 | V2 | V2/V1 | V2 | V2/V1 | ||
| 8.4.10-6 | 6.8.10-8 | 8.10-3 | 1.8.10-8 | 2.2.10-3 | 4.8.10-9 | 5.7.10-4 | |
| 2.3.10-4 | 1.9.10-5 | 8.2.10-2 | 7.2.10-6 | 3.10-2 | 2.7.10-6 | 1.1.10-2 | |
| 5.10-4 | 7.10-5 | 1.4.10-1 | 2.8.10-5 | 5.6.10-2 | 1.1.10-5 | 2.3.10-2 |
Оскільки енергія утворення у дивакансій більша, чим у вакансій, концентрація перших росте з температурою швидше. Таким чином, хоча при низьких T значення V2 набагато менше чим V1, при рості температури наближається до V1.
Якщо загартування проводиться при Tg більш високій чим температура, яка відповідає перетину кривої V2/V1 з рівнем концентрації 10-2, то більш ~10% уже є дивакансій. Оскільки на початкових стадіях загартування вакансії дуже рухливі, то може відбутись їх об’єднання. Келлер одержав приблизну оцінку можливості об’єднання вакансій в процесі загартування, допускаючи, що загальне число вакансій є постійним. Уже при високих швидкостях загартування великий процент моновакансій об’єднуються в дивакансії.
Внаслідок високої рухливості вакансій при високих температурах, частина моновакансій може губитись і на стоках. Ломер теоретично розглянув цей процес. При деякій T швидкість втрат вакансій за рахунок дифузії до фіксованого числа стоків виражається так
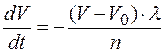 , (3.1.3)
, (3.1.3)
де V - вакансія в момент t в процесі загартування, V0- термодинамічна рівноважна концентрація вакансій при T, яка відповідає моменту часу t, l - частота стрибків вакансій при T, n - середнє число стрибків, яке повинна здійснити вакансія для досягнення стоку. Концентрацію V0 можна знайти із співвідношення 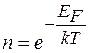 , якщо знехтувати ентропійною складовою, тоді
, якщо знехтувати ентропійною складовою, тоді
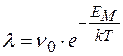 , (3.1.4)
, (3.1.4)
де n0-середня частота коливань.
Підставляючи (3.3) в (3.4) отримаємо
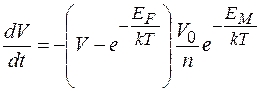 (3.1.5)
(3.1.5)
Якщо вважати, що охолодження відбувається по експоненційному закону охолодження, тобто
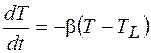 , (3.1.6)
, (3.1.6)
де ТL - температура, до якої охолоджується зразок, b - константа охолодження. Міняючи змінну t®T отримаємо співвідношення:
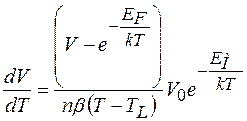 (3.1.7)
(3.1.7)
Інтегруючи (3.1.7) в границях від Tg до TL можна знайти V при довільній температурі T. Числові значення цього інтегралу при 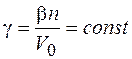 для деяких Tg можна знайти із рис.3.1.1
для деяких Tg можна знайти із рис.3.1.1
Із рис.3.1.2 слідує, що при T°=900°C і при великому g, яка відповідає високій швидкості охолодження або великому n зберігаються майже всі вакансії. Велике значення n відповідає добре відпаленому кристалу, або низькій концентрації стоків. Треба відзначити, що розподіл створених загартуванням вакансій не являється випадковим. Келер розглянув цю проблему з точки дифузії вакансій до циліндричних дислокацій. Розрахунки показали, що після швидкої високотемпературного загартування відхилення від випадкового розподілу не є вартим уваги. Тобто, при швидкому загартуванні найкраще зберігаються вакансії і найменше їх число об’єднається в комплекси. Проте, як правило, загартування завжди приводить до виникнення термічних напруг, так як зовнішні і внутрішні частини зразка нагріваються неоднаково. Якщо термічні напруги стають достатні, щоб викликати пластичну деформацію, то в зразку виникають дислокації, що можуть рухатись.
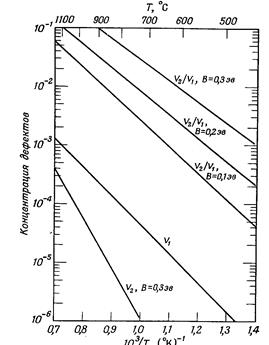
Рис.3.1.1. Концентраційні залежності вакансій від температури.
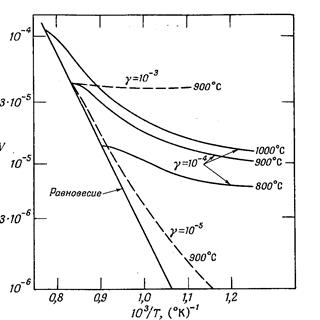
Рис.3.1.2. Визначення оптимальних режимів загартування.
При переміщені дислокацій утворюються дефекти, але механізм їх виникнення не є термодинамічним. Самі по собі дислокації є стоками для точкових дефектів і понижують ефективність загартування. Тому швидкість загартування зменшують до величини, нижче якої не виникає пластичної деформації.
Ван Бюрен [ ], беручи за основу теорію термічних напруг, вивів формули для максимальної швидкості загартування і розмірів зразка, при яких не виникає пластичної деформації. Умови, яким повинна задовольняти швидкість охолодження 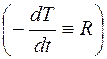 або радіус дроту r, такі:
або радіус дроту r, такі:
R<Rmax, 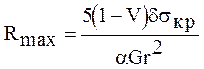 (3.1.8)
(3.1.8)
r<rmax, 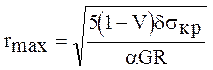
де R - швидкість загартування, r - радіус дроту, d - температуропровідність, a- коефіцієнт теплового розширення, sкр- критична напруга зсуву і G-модуль зсуву. Для ряду металів отримані наступні дані:
Метал Rmax .104°C/сек rmax,мм
r=0.1мм R=104°C/сек
Cu 1.7 0.13
Au 2.4 0.16
Із рис.3.1.2 слідує, що при T=900°C збереження вакансії можливе при g=10-3. Швидкості загартування g і R мають різний зміст так як вони відносяться до двох різних законів охолодження. Проте зрівняти їх можна, якщо прирівняти постійну швидкість в лінійному законі охолодження до початкової швидкості експоненційного охолодження. Якщо золотий дріт діаметром r=0.1мм охолоджується від 900 до 0°C , то
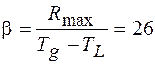 ,
,
оскільки g=nb/V0 і V0 ~1013, можна визначити n, необхідне для збереження вакансій, при g=10-3 n=4.108. Таке значення числа стрибків, яке здійснює вакансія до анігіляції відповідає низькій густині дислокацій, тобто добре відпаленій дротині.
Контрольні питання
1. Який фізичний механізм утворення точкових дефектів при загартуванні?
2. Яким чином утворення дивакансій впливає на процес загартування?
3. Пояснити механізм втрат вакансій через дифузійні процеси.
4. Яким співвідношенням пов’язані максимальна швидкість охолодження та розміри зразка з ефективністю загартування?
5. Як визначити оптимальні температурні режими загартування ?
6. Яку приблизно кількість стрибків здійснює вакансія до анігіляції у добре відпаленому зразку?
Дата добавления: 2020-07-18; просмотров: 581;











