Уравнение неразрывности движения потока
При обтекании тела частицы воздуха совершают сложное движение: поступательное, вращательное и деформационное (меняется форма и объем). С этим связаны типы обтекания: безвихревое (ламинарное) и вихревое (турбулентное) [20].
Уравнение неразрывности движения потока в математическом смысле представляет собой закон сохранения массы (основной закон природы) [20].
Это значит, что масса m в объеме W неизменна, то есть
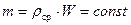 , или:
, или: 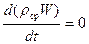 . (2.12)
. (2.12)
Однако каждая составляющая ρ и W могут при этом изменяться:
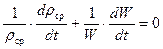 . (2.13)
. (2.13)
Последнее выражение и есть общее уравнение теории неразрывности движения потока жидкой среды (воздух, вода и т.п.). Частный случай общего уравнения – это установившееся движение, когда 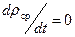 . Это относится и к несжимаемой жидкости.
. Это относится и к несжимаемой жидкости.
Рассмотрим течение жидкости через отдельную струйку.

Рис. 2.4. Течение жидкости через струйку
Количество жидкости, поступающее в единицу времени в объем через торцевое сечение I площадью S1 и равное ρ1v1S1, будет таким же, как масса жидкости ρ2v2S2, вытекающая через противоположное сечение II площадью S2, то есть:
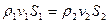 или
или 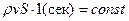 (2.14)
(2.14)
Последнее уравнение представляет собой уравнение массового расхода жидкости (воздуха), секундный расход. Для контроля определим размерность уравнения массового расхода:
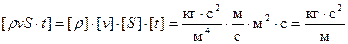 – размерность массы в технических единицах. Для несжимаемой жидкости v1S1 = v2S2, когда
– размерность массы в технических единицах. Для несжимаемой жидкости v1S1 = v2S2, когда  , а
, а  .
.
Рассмотренная гипотеза практически используется при обосновании характера обтекания тела в потоке, при обосновании формулы подъемной силы крыла, флюгарки ДАУ.
2.5. Подъемная сила. Теорема Николая Егоровича Жуковского [17, 18, 20, 21]
На рисунке 2.5 представлено крыло в потоке воздуха, расположенное к оси потока под углом атаки α. Здесь Y – подъемная сила, Q – лобовое сопротивление, которое в 20 – 25 раз меньше подъемной силы Y.
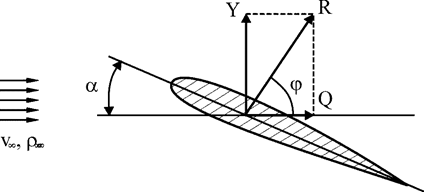
Рис. 2.5. Крыло в потоке воздуха
В 1906 году Н.Е. Жуковский для крыла бесконечного размаха доказал теорему о том, что на такое тело (при наличии циркуляции Г вокруг него) действует подъемная сила Y. Закон основан на применении закона количества движения к массам жидкости, обтекающего крыло.
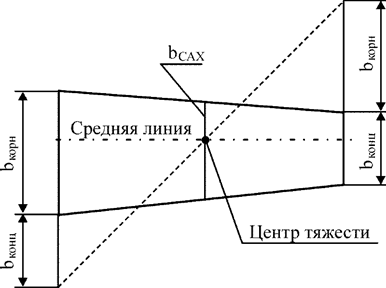
| Рис. 2.6. Геометрические характеристики крыла: bкорн – корневая хорда; bконц – концевая хорда; bСАХ – средняя аэродинамическая хорда |
Н.Е. Жуковский рассматривал крыло бесконечного размаха, у которого отношения корневой хорды (bкорн) к концевой хорде (bконц) равно бесконечности, то есть при bконц ≈ 0 или: bкорн/ bконц ≈ ∞ [17, 18, 20, 21].
Теорема Жуковского формулируется следующим образом: если поток, имеющий в бесконечности скорость v∞ и плотность ρ∞, обтекает цилиндрическое тело (крыло) и циркуляция скорости вокруг этого тела равна Г, то на тело со стороны жидкости будет действовать сила Y, перпендикулярная направлению скорости v∞ и равная произведению циркуляции на плотность и скорость потока в бесконечности [17].
Математически теорема Жуковского может быть записана формулой:
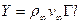 , (2.15)
, (2.15)
где l – длина части крыла бесконечного размаха, подъемную силу которой хотят определить.
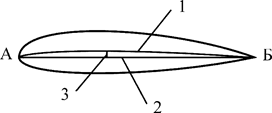
| Рис. 2.7. Геометрические параметры профиля крыла: 1 – средняя линия; 2 – хорда; 3 – кривизна абсолютная |
Величина циркуляции была предложена Жуковским в виде
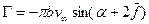 , (2.16)
, (2.16)
где b – хорда профиля крыла, α – угол атаки крыла в радианах, 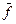 – относительная кривизна профиля крыла (т.е. отношение кривизны к хорде).
– относительная кривизна профиля крыла (т.е. отношение кривизны к хорде).
Подставив последнее выражение (2.16) в предыдущее (2.15) получим:
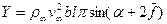 . (2.17)
. (2.17)
Положив bl = S (площадь крыла), 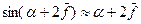 в радианах, с учетом того, что суммарный угол
в радианах, с учетом того, что суммарный угол 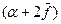 обычно не превышает 15˚ ≈ 0,26 радиана, будем иметь:
обычно не превышает 15˚ ≈ 0,26 радиана, будем иметь:
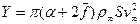 . (2.18)
. (2.18)
Как показала дальнейшая практика определения подъемной силы, выведенная теоретическая зависимость не полностью отражает действительность. Связано это с тем, что при выводе не был учтен пограничный слой вокруг крыла. В начале зарождения теории полета практика обгоняла теорию.
Как уже было сказано, для продувок аэродинамических тел в авиации служат аэродинамические трубы, в которых определяются реальные характеристики, в том числе и подъемные силы и силы лобового сопротивления конкретных тел.
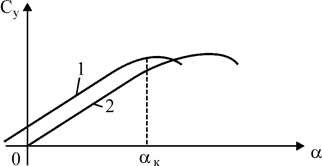
| Рис. 2.8. График зависимости безразмерного коэффициента подъемной силы Су от угла атаки α: 1 – несимметричное тело; 2 – симметричное тело |
На рисунке 2.8 приведена зависимость коэффициента подъемной силы Су от угла атаки. Практически подъемная сила определяется по формуле
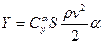 . (2.19)
. (2.19)
Коэффициент 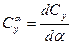 и зависит от многих конструктивных параметров обтекаемого тела (крыла):
и зависит от многих конструктивных параметров обтекаемого тела (крыла):
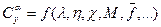 , (2.20)
, (2.20)
где λ – удлинение крыла, λ = l2/S; l – длина крыла; S – площадь крыла; η – сужение крыла, η = bкорн / bконц, bкорн – корневая хорда, bконц – концевая хорда крыла; χ – стреловидность крыла; М – число Маха; 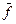 – относительная кривизна крыла.
– относительная кривизна крыла.
Для крыла с большим удлинением (λ > 2) и сужением (крыло бесконечного удлинения) все перечисленные параметры имеют существенное влияние на величину коэффициента 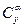 . Однако для крыла с малым удлинением коэффициент
. Однако для крыла с малым удлинением коэффициент 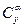 в основном зависит от удлинения. При этом малым удлинением считается величина
в основном зависит от удлинения. При этом малым удлинением считается величина 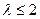 .
.
У крыльев бесконечного размаха по опытным данным коэффициент 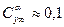 1/град ≈ 5,7 1/радиан. Для крыльев конечного размаха этот коэффициент меньше. Зная значение
1/град ≈ 5,7 1/радиан. Для крыльев конечного размаха этот коэффициент меньше. Зная значение 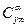 можно теоретически определить значение коэффициента подъемной силы для любого удлинения:
можно теоретически определить значение коэффициента подъемной силы для любого удлинения:
 , (2.21)
, (2.21)
где τ – поправочный коэффициент, равный τ ≈ 0,18.
Для точного определения значения всех коэффициентов крыло продувается в аэродинамической трубе.
Для крыла малого удлинения типа флюгарки коэффициент 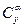 имеет следующую зависимость при М < 1:
имеет следующую зависимость при М < 1:
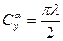 . (2.22)
. (2.22)
В таблице 2.3 со звездочкой приведены практические значения 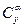 , а без звездочки по формуле (2.22).
, а без звездочки по формуле (2.22).
Таблица 2.3
| Λ | 0,5 | 1,0 | 1,5 | 2,0 | 3,0 |
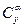 , рад , рад
| 0,9* 0,8 | 1,6* 1,57 | 2,1* 2,35 | 2,6* 3,14 | 3,2* |
Формула пересчета (2.21) мало пригодна для крыльев с малым удлинением, но хорошо приемлема для крыльев с большим удлинением (λ > 2). У крыльев с малым удлинением коэффициент 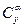 значительно меньше коэффициента крыла с большим удлинением.
значительно меньше коэффициента крыла с большим удлинением.
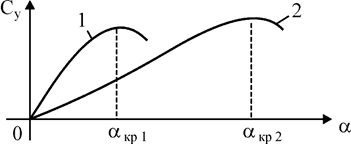
| Рис. 2.9. Сравнение кривых Су (α) пластин больших и малых удлинений: 1 – λ > 2; 2 – λ < 2 |
Теорема Жуковского явилась основой теории полета и аэродинамики крыла. Она отвечает на вопрос: "Почему самолет летает?" Теорема Жуковского вместе с гипотезой о неразрывности движения потока объясняет принцип образования подъемной силы крыла самолета, особенности восприятия статического давления в ПВД и др.
На рисунке 2.10 показано крыло в потоке воздуха. Показано, что под крылом давление больше по сравнению с давлением над профилем крыла. Струи воздуха чтобы соединится в одной точке (разрыв не допустим) после прохождения крыла должны двигаться с разными скоростями, так как их пути следования разные. Верхний слой движется с большей скоростью, а значит давление над крылом меньше давления под крылом. Разность давления, умноженная на площадь крыла, создает подъемную силу.
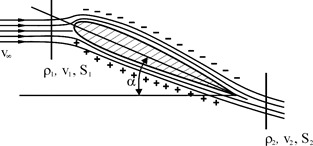
| Рис. 2.10. Характер обтекания крыла в потоке воздуха, установленного под углом атаки α к потоку: - - - - – давление над крылом; + + + + – давление под крылом |
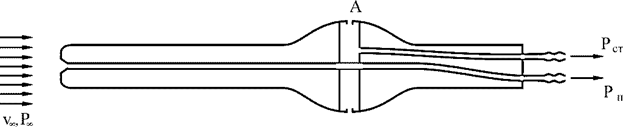
Рис. 2.11. Гофрированное тело в потоке воздуха
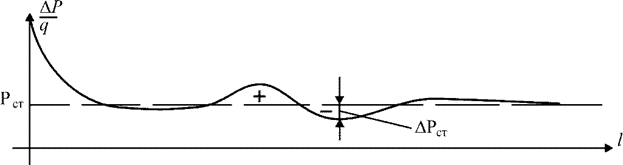
Рис. 2.12. Распределение избыточного давления по поверхности гофрированного тела в потоке воздуха
На переднем участке, на гладком цилиндре используется принцип Пито, когда в лобовом отверстии воспринимается полное давление Рп, а на гладких параллельных потоку стенках прибора с отверстиями воспринимается статическое давление Рст.
Эффект ребристой поверхности используется в авиаприборостроении для компенсации погрешностей восприятия статического давления при помощи ПВД.
Например, если в месте установления ПВД на самолете погрешность имеет плюсовой знак, то для компенсации ее нужно взять статическое давление от камеры А с отрицательной погрешностью.
Это же явление используется для повышения чувствительности измерителя приборной скорости. И в этом случае статическое давление нужно взять в камере А. Тогда динамическое давление 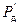 сформируется следующим образом:
сформируется следующим образом:
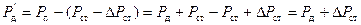 (2.23)
(2.23)
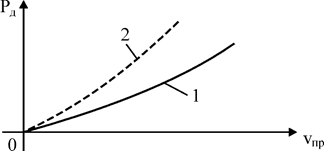
| Рис. 2.13. График динамического давления в зависимости от скорости: 1 – кривая до компенсации; 2 – кривая после компенсации с помощью гофрированного тела |
На графике 2.13 видно, что новая кривая 2 круче стандартной кривой 1.
Идеально шар в потоке не имеет подъемной силы, если он не вращается. Стоит его закрутить, как появляется подъемная сила.
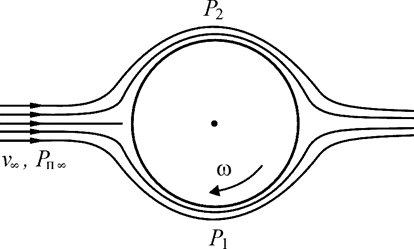
Рис. 2.14. Шар в потоке воздуха
При вращении ω шар будет иметь подъемную силу, так как Р1 > Р2. Это объясняется тем, что в верхней точке движение потока ускоряется, а в нижней точке замедляется.
Приведенные здесь положения не действуют в свободномолекулярном потоке. Там применима теория Ньютона, ударная теория. Из этой теории следует, что образуется только сила лобового сопротивления, подъемная сила отсутствует, так как сплошности нет, гипотеза о неразрывности не действует, циркуляции вокруг тела нет. Но практически в отличие от теории Ньютона небольшая подъемная сила появляется. Аэродинамическое качество К = Сy/Сx в свободномолекулярном потоке при диффузионном отражении молекул мало. Так, при М = 1 К = 0,5, а при М = 20 К = 0,1. Это подтверждает факт того, что эффективность несущей поверхности летательного аппарата в разреженной атмосфере мала.
Дата добавления: 2020-07-18; просмотров: 590;











