Неустановившееся движение электропривода при постоянном динамическом моменте

Неустановившееся движение ЭП имеет место, когда моменты дви­гателя и нагрузки отличаются друг от друга, т. е. М≠М_с. В этом слу­чае динамический момент М_дин не равен нулю и происходит увеличе­ние или снижение скорости движения. Наиболее типичными приме­рами неустановившегося движения в ЭП являются пуск, торможение и реверс двигателя, его переходы с одной скорости на другую в про­цессе ее регулирования или изменения нагрузки на валу.

Неустановившееся движение возникает при переходе ЭП из ус­тановившегося движения с одними параметрами к установившему­ся движению с другими параметрами (если, конечно, движение ус­тойчивое). По этой причине неустановившееся движение называют также переходным процессом или переходным режимом ЭП.

Целью рассмотрения неустановившегося движения является по­лучение зависимостей механических переменных (координат) ЭП – моментов, скорости и угла поворота вала двигателя от времени. Рассмотрим переходные процессы в механической части ЭП, обус­ловленные инерционностью движущихся элементов. Иногда такие процессы называют механическими [1].

Искомые зависимости получим решением (интегрированием) дифференциального уравнения механического движения (45), а также дифференциального уравнения Ω = dφ/dt, связывающего угол поворота φ вала двигателя и его скорость Ω.

Для решения этих уравнений необходимо знать законы изменения моментов двигателя и нагрузки, а также массы и моменты инерции движущихся элементов и начальные (нулевые) значения переменных.

В общем случае моменты двигателя и нагрузки, а иногда и мо­мент инерции могут являться функциями времени, скорости и по­ложения ИО (угла поворота вала двигателя).

Из всего многообразия возможных переходных процессов рас­смотрим наиболее часто имеющие место случаи, когда моменты двигателя и нагрузки ЭП являются постоянными величинами, не зависящими от скорости или времени, а моменты инерции и массы движущихся элементов не изменяются в переходных процессах. Другие возможные переходные процессы см. в [1 ].

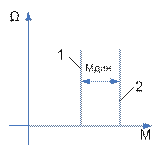
Рис.11. Механические характеристики двигателя (2) и исполнительного органа (1)

На рис. 11 приведены механические характеристики двигате­ля 2 и нагрузки (исполнительного органа) 7, при которых их мо­менты неизменны, т.е. динамический момент постоянен и положи­телен. Уравнение движения (46) в этом случае решается методом разделения переменных и ее решение имеет вид

Постоянная интегрирования С находится из начального условия переходного процесса: при t =0 Ω = Ω _нач. Подставляя это условие в (53), получим С = Ω _нач. Тогда окончательно (53) принимает вид

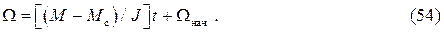
Полученная формула показывает, что при разбеге ЭП (см. рис. 11) скорость Ω линейно зависит от времени. При (М - М_с) > 0 скорость увеличивается (прямая 4), а при (М - М_с) < 0 – снижается. Мо­мент двигателя от времени не зависит, поэтому зависимость М(t) изображается прямой линией 3.

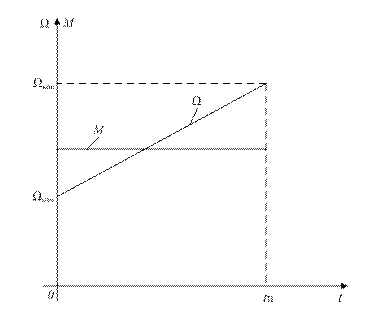
Рис.12. График переходного процесса разбега ЭП: М - динамический момент, Ω -угловая скорость вращения

Время переходного процесса t_п.п, за которое скорость изменится от некоторого начального Ω _нач до конечного Ω_кон уровня, определя­ется из (54) при подстановке в нее t = t_{п. п} и Ω = Ω _кон:

t_{п. п}=J(Ω _кон- Ω _нач)/(М - М_с). (55)

Задача 9. Рассчитать и построить зависимость Ω(t) при следующих исход­ных данных: М= 50 Нм; М_c= 100 Нм; J= 0,1 кг•м²; Ω_нач= 100 рад/с. Рассчитать время переходного процесса, за которое скорость снизится в два раза.

Задача 10. Определить динамический момент, который при J=0,2 кг·м² обеспечит увеличение скорости на 200 рад/с за время t_{п. п}= 1 с.

Задача 11. Получить общее выражение для определения зависимости угла поворота вала двигателя от времени φ(t) для случая постоянного динамическо­го момента и оценить вид этой зависимости.

2.7. Неустановившееся движение при линейных механических характеристиках двигателя и исполнительного органа [1]

При линейных механических характеристиках двигателя и ис­полнительного органа динамический момент ЭП также линейно за­висит от скорости. Такие переходные процессы характерны для ЭП с двигателями постоянного тока независимого возбуждения, а так­же двигателями, характеристики которых могут быть частично или полностью представлены (аппроксимированы) прямыми линиями.

На рис.13, а показаны линейные механические характерис­тики двигателя 1 и исполнительного органа 2, построенные по следующим алгебраическим уравнениям:

М = М_кз - βΩ; (56)

М =М_со + β_сΩ,

где М_кз и М_с0 – моменты двигателя и исполнительного органа при нулевой скорости.

Подставляя эти выражения в уравнение движения (36), получим

М-М_с=М_кз- βΩ - М_со - β_сΩ =J(dΩ/dt). (57)

В обычной для дифференциальных уравнений форме уравнение (57) бу­дет иметь вид

Т_м(dΩ /dt) + Ω = Ω _уст, (58)

где Т_м =J/(β + β_с) – электромеханическая постоянная времени, с;

Ω_уст = (М_кз-М_со)/(β+β_с) – установившаяся скорость, соответству­ющая точке пересечения характеристик двигателя и исполнитель­ного органа.

Выражение (58) по своей форме является линейным неоднород­ным дифференциальным уравнением первого порядка, решение ко­торого Ω (t) имеет вид

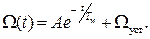(59)

Постоянный коэффициент А определяется из начальных усло­вий переходного процесса: при t = 0 Ω = Ω _нач, т. е. А = Ω _нач - Ω _уст.

Тогда окончательно зависимость изменения скорости от време­ни будет иметь вид

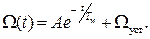
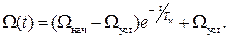(60)

Запишем момент двигателя в функции времени, исходя из (56):

M(t) = M_кз-βΩ(t). (61)

С учетом того, что

β=ΔМ/ΔΩ =(М_кз - М_уст)/Ω _уст=(М_кз – М_нач) /Ω _нач

после подстановки Ω _нач и Ω _уст получим

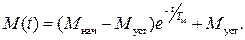(62)

В распространенном для ЭП случае, когда β_с=0 (характерис­тикой исполнительного органа является вертикальная прямая ли­ния), входящие в (60) и (62) параметры будут иметь упрощен­ный вид

Т_м=J/β=JΩ ₀/М_кз;

Ω _уст=(М_кз-М_с)/β.

Время переходного процесса t_{п. п}, за которое скорость двигателя изменится от некоторого начального значения Ω _нач до конечного Ω _кон, определяется в этом случае логарифмированием (60):

t_п.п=T_мln[(Ω _уст- Ω _нач)/(Ω _уст- Ω _кон)]=

=T_мln[(M_уст-M_нач)/(M_уст-M_кон)]. (63)

Анализ полученных выражений (60) и (62) показывает, что скорость и момент двигателя изменяются во времени по экспонен­циальному закону с постоянной времени T_м. На рис. 13, б показа­ны графики переходного процесса разбега: Ω (t) – кривая 3 и М(t)- кривая 4,при увеличении скорости двигателя от Ω _нач до Ω_уст. Отме­тим, что начальные и установившиеся уровни скорости и момента определяются из рис. 13, а, отражая связь установившегося и пере­ходного движений ЭП.

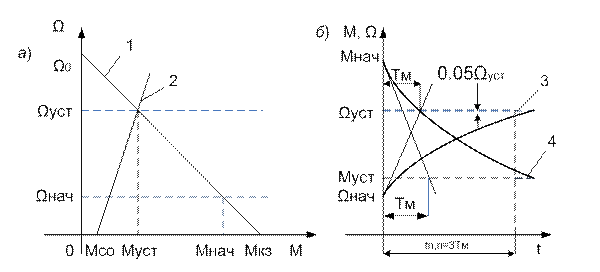
Рис.13.Линейные механические характеристики двигателя и исполнительного органа (а) и график переходного процесса разбега ЭП (б)

Как следует из (63), время достижения установившихся уров­ней скорости и момента (т.е. время переходного процесса) является бесконечно большим. Поэтому в технических расчетах используют так называемое практическое время переходного процесса, прини­маемое обычно равным трем постоянным времени, т.е. t_п.п = 3T_м. За этот интервал времени скорость достигает 95% своего установив­шегося значения.

Постоянная времени Т_м имеет определенное графическое и фи­зическое выражение. На рис. 13, б она равна отрезку, отсекаемому касательной, проведенной к кривой переходного процесса в точке t = 0 на горизонтальной прямой, соответствующей установивше­муся значению переменной (скорости или момента). Количествен­но Т_м равна времени разгона t двигателя без нагрузки (М_с = 0) из неподвижного состояния (Ω_нач = 0) до скорости идеального холос­того хода Ω₀ = Ω_уст под действием пускового момента М_кз. Действи­тельно, из формулы (55) для указанных условий следует, что

t_п.п=t_р=JΩ ₀/М_кз=Т_м.

Задача 12. Выполнить расчет и построение кривых переходного процесса Ω(t) и M(t) при линейной механической характеристике двигателя и следующих исходных данных: Ω_нач = 0; Ω_уст= 150 рад/с, М_нач = М_к.з= 150 Нм; Ω₀= 200 рад/с; М_уст = М_с = 40 Нм; J=0,1 кг·м². Оценить практическое время переходного процесса.

Задача 13. Рассчитать и построить зависимости Ω(t) и M(t) для двигателя, механическая характеристика которого приведена на рис.14, если М_с=0, Ω_нач =200 рад/с.

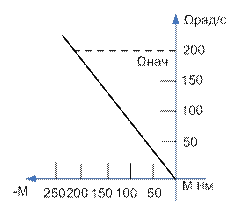
Рис.14. Механическая характеристика к задаче 13

Задача 14. Двигатель, механическая характеристика 3 которого приведе­на на рис.15, работая в установившемся режиме (точка А), преодолевал мо­мент сопротивления М_с1 = 150 Нм. В момент времени t = 0, принимаемый за начало отсчета, произошло скачкообразное изменение момента нагрузки (пря­мые 1, 2) до уровня М_с2 = 250 Нм (точка Б). Рассчитать и построить зависимо­сти Ω(t) и M(t), соответствующие этому увеличению нагрузки.

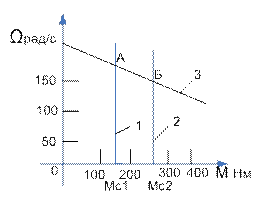
Рис.15. Механические характеристики к задаче 13

Вопросы для самоконтроля

1. Напишите полные уравнения движения для вращательного и поступательного характера движения. 2. Преобразуйте полные уравнения движения в упрощенные, обоснуйте возможность этого преобразования.

3. Приведите уравнения двухмассовой системы ЭП, дайте пояснения параметрам этого уравнения.

4. Нарисуйте механические характеристики двигателей постоянного тока с независимым и последовательным возбуждением, асинхронного двигателя и синхронного двигателя.

5. Нарисуйте механические характеристики исполнительных органов рабочих машин, соответствующие работе с постоянным моментом (с характером нагрузки типа «сухое трение»), с постоянной мощностью, с вентиляторным характером нагрузки и с характером нагрузки типа «вязкое трение».

6. Как оценить жесткость механических характеристик двигателя и исполнительного органа рабочей машины.

7. Напишите формулу проверки устойчивости работы ЭП.

8. Нарисуйте график переходного процесса разбега ЭП при постоянном и положительном значении динамического момента.

9. Дайте определение понятию «практическое время переходного процесса».

10. Нарисуйте график переходного процесса разбега ЭП при линейных механических характеристиках двигателя и исполнительного органа. Поясните методику определения электромеханической постоянной времени ЭП по характеристикам, приведенным на этом графике.

3. РЕГУЛИРОВАНИЕ КООРДИНАТ ЭЛЕКТРОПРИВОДА [1]

Для обеспечения требуемых режимов работы машин, производ­ственных механизмов и самого ЭП некоторые переменные, кото­рые характеризуют их работу, должны регулироваться. Такими пе­ременными, часто называемыми в ЭП координатами, являются, например, скорость, ускорение, положение ИО или любого друго­го механического элемента привода, токи в электрических цепях двигателей, моменты на их валу и др.

Типичным примером необходимости регулирования координат может служить ЭП пассажирского лифта. При пуске и остановке кабины лифта для обеспечения комфортности пассажиров ускоре­ние и замедление ее движения ограничиваются. Перед остановкой скорость кабины должна снижаться, т. е. регулироваться. И, нако­нец, кабина с заданной точностью должна останавливаться на тре­буемом этаже. Такое управление движением кабины лифта обеспе­чивается за счет регулирования соответствующих координат (пере­менных) ЭП лифта.

Отметим, что процесс регулирования координат движения все­гда связан с получением искусственных (регулировочных) характе­ристик двигателя, что достигается целенаправленным воздействи­ем на двигатель. Рассмотрим подробнее регулирование основных координат ЭП.