Включение в цепь r, C к источнику постоянного напряжения.

Пусть при t=0 незаряженная емкость С подключается через резистор r к источнику постоянного напряжения u(t)=U (нулевые начальные условия uC(0)=0) (рис 5.6)

По второму закону Кирхгофа уравнение для послекоммутационного периода (tі0) имеет вид

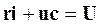
где i, uc - соответственно переходной ток в цепи и переходное напряжение на емкости. С учетом того, что i=C·duc/dt получаем дифференциальное уравнение рассматриваемой цепи

(5.21)

Решение этого уравнения, согласно (5.3), известно

(5.22)

Первое слагаемое u_спр=U - частное решение уравнения (5.21), выражает принужденное значение, когда емкость зарядиться до напряжения источника. Второе слагаемое uC_св=A·exp(pt) - решение однородного дифференциального уравнения, полученные из (5.21), и содержит корень характеристического уравнения, равный для этой цепи p=-1/(rC), и постоянную интегрирования А, вычисляемую из начальных условий. Для любой цепи с резистором и емкостью они устанавливают на основании второго закона коммутации. Так при t=0 из (5.22) находим

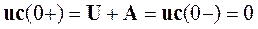(5.23)

отсюда А=-U и переходное напряжение на емкости будет изменяться по закону

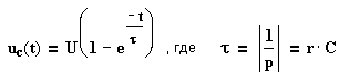(5.24)

Для тока получим

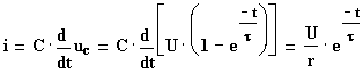(5.25)

Кривые изменения тока приведены на рис 5.7

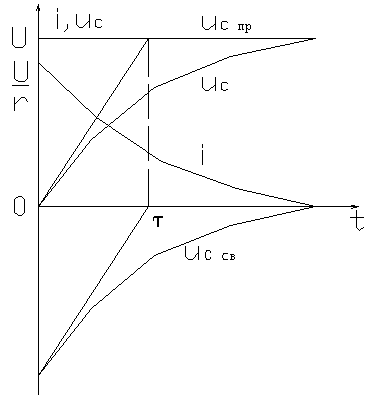Рис 5.7