Ход лучей в выпуклом зеркале. Сферическая аберрация

Ход лучей в выпуклом зеркале. 1) Шайба Гартля (или прибор Кольбе). 2) Выпуклое зеркало (№ 3 из набора). 3) Источник света.

Выпуклое цилиндрическое зеркало устанавливается на шайбе так же и таким же« приемом, как и вогнутое (опыт 3). При этом надо иметь в виду, что выпуклое зеркало рассеивает падающие на него лучи, поэтому на шайбе полоска отраженного света будет становиться все шире по мере удаления от зеркала. Такой отраженный луч можно проследить лишь на малом расстоянии (рис. 266, /). Демонстрируются три случая хода лучей.

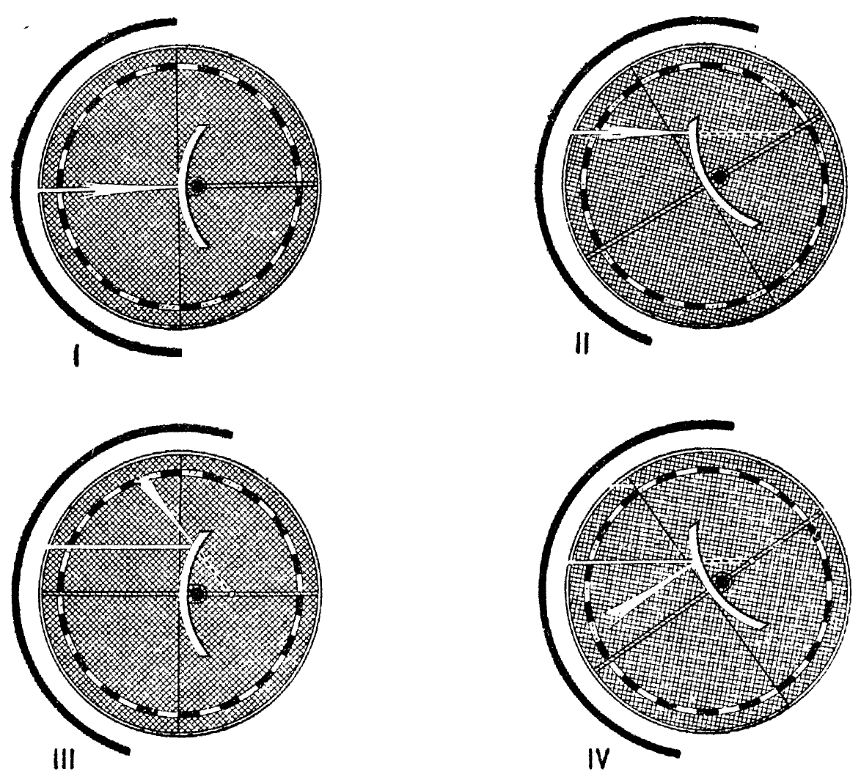
Рис. 266. Шайба Гартля (ход лучей в выпуклом зеркале)

Случай 1. Луч, продолжение которого проходит через геометрический центр зеркала, после отражения идет по тому же направлению.

Поворотом ширмы и шайбы направляют падающий луч так, чтобы отраженный луч совпал с падающим. Повторив такую установку несколько (3—4) раз, убеждаются, что продолжения падающих лучей за зеркало проходят через одну и ту же точку — геометрический центр зеркала (рис. 266, II). Полезно положение центра заранее наметить на шайбе.

Случай 2. Если падающий луч идет параллельно главной оптической оси (или соответственно основной установке — параллельно нулевому диаметру), то продолжение отраженного луча проходит через мнимый фокус, лежащий за зеркалом (на главной оси) на середине радиуса (рис. 266, III). Положение фокуса полезно заранее отметить карандашом на шайбе.

Случай 3. Луч, продолжение которого проходит через фокус, после отражения идет параллельно главной оптической оси.

Щель и шайбу устанавливают так, чтобы отраженный луч шел параллельно нулевому диаметру; тогда при всех повторениях этой установки продолжения падающих лучей за зеркало пройдут через одну и ту же точку — фокус зеркала (рис. 266, IV), положение фокуса было найдено в случае 2.

Собирание и рассеивание лучей сферическими зеркалами. 1) Шайба Гартля (или прибор Кольбе). 2) Вогнутое и выпуклое зеркала. 3)Источник света.

Установив вогнутое зеркало на шайбе, открывают несколько щелей (3 или 5) и направляют пучок параллельных (или слабо расходящихся) лучей на зеркало вдоль его оптической оси; все отраженные лучи сходятся в одной точке — в фокусе зеркала или близ него (рис. 267, /).

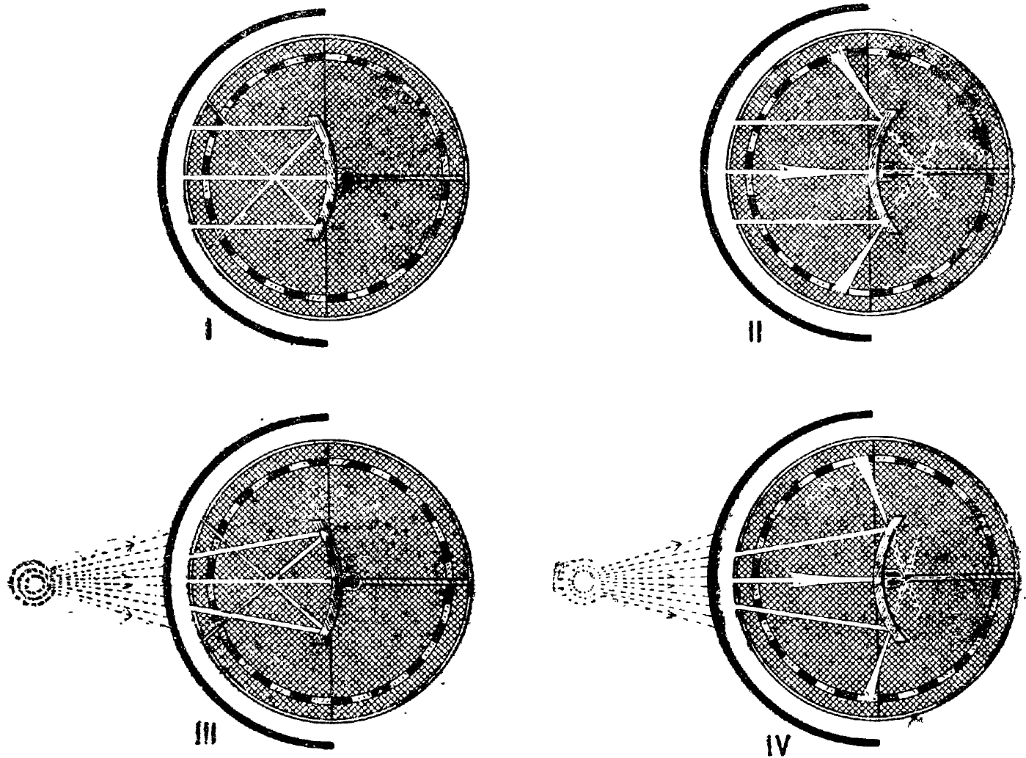
Рис. 267. Шайба Гартля (ход лучей в сферических зеркалах)

В случае выпуклого зеркала отраженные лучи расходятся во все стороны, но если все лучи продолжить за зеркало, то эти продолжения тоже сойдутся в одной точке — в мнимом фокусе зеркала (рис. 267, II) или близ него (если падал пучок слабо расходящихся лучей).

Если взять пучок сильно расходящихся лучей (§ 25, 1 и 2) так, что можно наметить положение светящей точки, лежащей недалеко от шайбы, то точка, где сойдутся лучи, отраженные от вогнутого зеркала, будет являться действительным изображением светящей точки (рис. 267, III), или точка, где сойдутся продолжения лучей, отраженных от выпуклого зеркала, будет служить мнимым изображением светящей точки (рис. 267, IV).

Сферическая аберрация. В опыте 5 применялись центральные лучи, идущие параллельно оптической оси (или под небольшим углом к ней) и падающие на зеркало недалеко от его середины. Повторяют тот же опыт, но берут крайние лучи, падающие на края зеркала далеко от его середины (в этом случае нулевой диаметр уже не совпадает с оптической осью).

Опыт показывает, что при таком условии отраженные лучи в случае вогнутого зеркала (рис. 268, I) и продолжения лучей в случае выпуклого зеркала (рис. 268, II) не сходятся в одной точке, обнаруживая явление сферической аберрации. При этом надо показать, что чем более к краю падает луч, тем ближе к зеркалу идет отраженный луч. Чтобы легче было отличать лучи друг от друга, полезно сделать лучи разноцветными, вставив на место вынутых задвижек полоски цветных стекол.

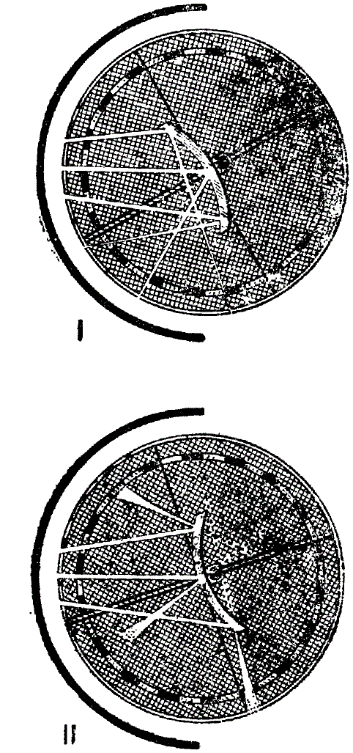
Рис. 268. Шайба Гартля (сферическая аберрация при отражении от сферических зеркал)

Если на вогнутое зеркало падают не отдельные лучи, а целый поток света шириной во все отверстие зеркала, то вследствие аберрации все точки пересечения соседних отраженных лучей располагаются на так называемой фокальной поверхности характерной формы с остроконечной вершиной, лежащей в фокусе зеркала.

Пересекая фокальную поверхность плоскостью экрана, получим в сечении кривую особой формы (рис. 269); эта кривая называется каустической (зажигательной). Ее можно увидеть, если направить солнечные лучи на вогнутую жестяную полоску, поставленную на лист бумаги, или осветить внутренность полированного круглого сосуда.