Расчёт косозубой цилиндрической передачи (тихоходная ступень) Пример расчета.

Выбор твёрдости, термообработки и материала колёс

Выбираем марку стали: для шестерни – 40Х, твёрдость ≤ 350 НВ₁; для колеса – 40Х, твёдость ≤ 350 НВ₂. Разность средних твёрдостей НВ_1ср – НВ_2ср = 20…50.

Определяем механические характеристики стали 40Х: для шестерни твёрдость 269…302 НB₁, термообработка – улучшение, D_пред = 125 мм; для колеса твёрдость 235…262 НВ₂, термообработка – улучшение, S_пред = 125 мм.

Определяем среднюю твёрдость зубьев шестерни и колеса:

HB_1ср = (269 + 302)/2 = 285,5;

HB_2ср = (235 + 262)/2 = 248,5.

Определение допускаемых контактных напряжений и

Напряжений изгиба для зубьев шестерни и колеса

Определим коэффициент долговечности:

K_HL = (N_H0/N)^1/6,

где N_H0 – число циклов перемены напряжений, соответствующее пределу выносливости; N – число циклов перемены за весь срок службы

N = 573wL_h,

где w – угловая скорость соответствующего вала, с^-1; L_h – срок службы привода, ч.

Так для колеса: N₂ = w₂L_h = 10,5×20000 = 120330000; N_H02 = 16,37×10⁶.

Для шестерни: N₁ = uN₂ = 2,34×120330000 = 281572200; N_H01 = 22,62×10⁶.

Коэффициент долговечности:

для шестерни K_HL1 = (22,62×10⁶/281572200)^1/6 = 0,657,

для колеса K_HL2 = (16,37×10⁶/120330000)^1/6 = 0,717.

Так как N₁ > N_H01, а N₂ > N_H02, то принимаем K_HL1 = 1, K_HL2 = 1.

Определяем допускаемое контактное напряжение, соответствующее пределу контактной выносливости при числе циклов перемены напряжений N_H0:

для шестерни [s]_Н01 = 1,8НВ_1ср + 67 = 1,8×285,5 + 67 = 580,9 Н/мм²;

для колеса [s]_Н02 = 1,8НВ_2ср + 67 = 1,8×248,5 + 67 = 514,3 Н/мм²;

Определяем допускаемое контактное напряжение:

для шестерни

[s]_Н1 = K_HL1[s]_Н01 = 1×580,9 = 580,9 Н/мм²,

для колеса

[s]_Н2 = K_HL2[s]_Н02 = 1×514,3 = 514,3 Н/мм².

Так как НВ_1ср – НВ_2ср = 285,5 – 248,5 = 37 = 20…50, то передачу рассчитываем по меньшему значению допускаемого контактного напряжения из полученных для шестерни и колеса. Таким образом:

[s]_Н = 514,3 Н/мм².

Коэффициент долговечности для вычисления напряжений изгиба:

K_FL = (N_F0/N)^1/6,

где N_F0 = 4×10⁶ – число циклов перемены напряжений для всех сталей, соответствующее пределу выносливости; N – число циклов перемены за весь срок службы.

Для шестерни K_FL1 = (4×10⁶/281572200)^1/6 = 0,492;

для колеса K_FL2 = (4×10⁶/120330000)^1/6 = 0,567.

Так как N₁ > N_F01, а N₂ > N_F02, то принимаем K_FL1 = 1, K_FL2 = 1.

Определяем допускаемое контактное напряжение, соответствующее пределу контактной выносливости при числе циклов перемены напряжений N_F0:

для шестерни [s]_F01 = 1,03НВ_1ср = 1,03×285,5 = 294,1 Н/мм²;

для колеса [s]_F02 = 1,03НВ_2ср = 1,03×248,5 = 256,0 Н/мм²;

Определяем допускаемое контактное напряжение:

для шестерни

[s]_F1 = K_FL1[s]_F01 = 1×294,1 = 294,1 Н/мм²,

для колеса

[s]_F2 = K_FL2[s]_F02 = 1×256,0 = 256,0 Н/мм².

Далее передачу рассчитываем по меньшему значению допускаемого напряжения изгиба из полученных для шестерни и колеса. Таким образом:

[s]_F = 256,0 Н/мм².

Проектный расчёт

Определим межосевое расстояние:

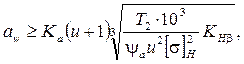
где К_а – вспомогательный коэффициент; y_a – коэффициент ширины венца колеса; K_Hb – коэффициент неравномерности нагрузки по длине зуба.

a_w ³ 43×(2,34 + 1)×(235×10³×1/(0,28×2,34²×514,3²))^1/3 = 119,74 мм,

Полученое значение округляем до стандартного a_w = 120 мм.

Определим модуль зацепления:

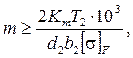
где К_m – вспомогательный коэффициент; d₂ = 2a_wu/(u + 1) – делительный диаметр колеса, мм; b₂ = y_aa_w – ширина венца колеса, мм.

m ³ 2×5,8×235×10³/(168,14×34×256,0) = 1,89 мм.

Полученное значения модуля округляем до стандартного m = 2 мм.

Минимальный угол наклона зубьев:

b_min = arcsin(3,5m/b₂) = arcsin(3,5×2/34) = 12,03°.

Суммарное число зубьев шестерни и колеса:

z_S = 2a_wcosb_min/m = 2×120×cos(12,03°)/2 = 117,37.

Полученное значение округляем в меньшую сторону до целого числа.

Уточняем действительную величину угла наклона зубьев:

b = arccos(z_Sm/(2a_w)) = arccos(117×2/(2×120)) = 12,85°.

Число зубьев шестерни:

z₁ = z_S/(1 + u) = 117/(1 + 2,34) = 35,0.

Полученное значение округляем до ближайшего целого числа z₁ = 35.

Число зубьев колеса:

z₂ = z_S – z₁ = 117 – 35 = 82.

Определяем фактическое передаточное число и его отклонение:

u_ф = z₂/z₁ = 82/35 = 2,34;

(|2,34 – 2,34|/2,34)×100% = 0,1 < 4 %.

Определим фактическое межосевое расстояние

a_w = (z₁ + z₂)m/(2cosb) = (35 + 82)×2/(2×cos12,85°) = 120,00 мм.

Делительные диаметры шестерни и колеса:

d₁ = mz₁/cosb = 2×35/cos12,85° = 71,8 мм;

d₂ = mz₂/cosb = 2×82/cos12,85° = 168,2 мм.

Диаметры вершин зубьев шестерни и колеса:

d_a1 = d₁ + 2m = 71,8 + 2×2 = 75,8 мм;

d_a2 = d₂ + 2m = 168,2 + 2×2 = 172,2 мм.

Диаметры впадин зубьев:

d_f1 = d₁ – 2,4m = 71,8 – 2,4×2 = 67,0 мм;

d_f2 = d₂ – 2,4m = 168,2 – 2,4×2 = 163,4 мм.

Определим силы в зацеплении:

окружная F_t = 2T₂×10³/d₂ = 2×235×10³/168,2 = 2794 Н;

радиальная F_r = F_ttan20°/cosb = 2794×0,364/cos12,85° = 1043 Н;

осевая F_a = F_ttanb = 2794×tan12,85° = 637 Н.

Проверочный расчёт

Проверим условие пригодности заготовок колёс:

D_заг = d_a1 + 6 = 75,8 + 6 = 81,8 мм < D_пред;

S_заг = b₂ + 4 = 34 + 4 = 38 мм < S_пред.

Условия выполнены.

Проверим контактные напряжения

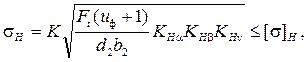
где К – вспомогательный коэффициент; К_Нa – коэффициент распределения нагрузки; K_Нb – коэффициент неравномерности нагрузки по длине зуба; К_Нv – коэффициент динамической нагрузки.

Окружная скорость колёс:

v = w₂d₂/(2×10³) = 10,5×168,2/2000 = 0,88 м/с.

Степень точности передачи равна 9.

Расчётное контактное напряжение:

s_Н = 376×((2794×(2,34 + 1)/(168,2×34))×1,1×1×1,01) = 509,5 < 514,3 Н/мм².

Полученное значение меньше допустимого на 0,9%, условие выполнено.

Проверим напряжения изгиба зубьев шестерни и колеса:

s_F2 = Y_F2Y_bF_tK_FaK_FbK_Fv/(b₂m) ≤ [s]_F2;

s_F1 = s_F2Y_F1/Y_F2 ≤ [s]_F1,

где K_Fa – коэффициент распределения нагрузки; K_Fb – коэффициент неравномерности нагрузки по длине зуба; K_Fv – коэффициент динамической нагрузки; Y_F – коэффициенты формы зуба шестерни и колеса; Y_b = 1 – b/140 = 0,91 – коэффициент наклона зуба.

s_F2 = 3,6×0,91×2794×1×1×1,04/(34×2) = 141,4 < 256,0 Н/мм²;

s_F1 = 141,4×3,72/3,6 = 146,1 < 294,1 Н/мм².

Условия выполнены.

Литература

1. Чернавский С.А., Боков К.Н., Чернин И.М., Ицкевич Г.М., Козинцов В.П. 'Курсовое проектирование деталей машин': Учебное пособие для учащихся. М.:Машиностроение, 1988 г. 416с.

2. Дунаев П.Ф. ,Леликов О.П. 'Конструирование узлов и деталей машин', М.: Издательский центр 'Академия', 2003. 496 c.

3. Березовский Ю.Н., Чернилевский Д.В., Петров М.С. 'Детали машин', М.: Машиностроение, 1983. 384 c.

4. Боков В.Н., Чернилевский Д.В., Будько П.П. 'Детали машин: Атлас конструкций.' М.: Машиностроение, 1983. 575 c.

5. Гузенков П.Г., 'Детали машин'. 4-е изд. М.: Высшая школа, 1986. 360 с.

6. Детали машин: Атлас конструкций / Под ред. Д.Р.Решетова. М.: Машиностроение, 1979. 367 с.

7. Дружинин Н.С., Цылбов П.П. Выполнение чертежей по ЕСКД. М.: Изд-во стандартов, 1975. 542 с.

8. Кузьмин А.В., Чернин И.М., Козинцов Б.П. 'Расчеты деталей машин', 3-е изд. - Минск: Вышейшая школа, 1986. 402 c.

9. Куклин Н.Г., Куклина Г.С., 'Детали машин' 3-е изд. М.: Высшая школа, 1984. 310 c.

10. 'Мотор-редукторы и редукторы': Каталог. М.: Изд-во стандартов, 1978. 311 c.

11. Перель Л.Я. 'Подшипники качения'. M.: Машиностроение, 1983.588 c.

12. 'Подшипники качения': Справочник-каталог / Под ред. Р.В. Коросташевского и В.Н. Нарышкина. М.: Машиностроение, 1984. 280 с.

13. 'Проектирование механических передач' / Под ред. С.А. Чернавского, 5-е изд. М.: Машиностроение, 1984