Технические свойства пищевых продуктов

В пищевой промышленности перерабатывают сырье и получают готовые продукты в различном агрегатном состоянии: твердом, жидком, паро- и газообразном. Для расчета процессов и аппаратов необходимо знать свойства пищевых продуктов и сырья.

Многие пищевые продукты представляют собой однородные и неоднородные смеси.

К однородным смесям относятся растворы, например сахарные, водно-спиртовые, соки и т. д. Однородные смеси характеризуются концентрацией растворенного вещества.

К неоднородным относятся смеси твердого вещества с жидкостью, а также смеси различных нерастворимых одна в другой жидкостей. Для характеристики неоднородных смесей вводят понятие объемной или массовой доли, например доли твердого вещества в жидкости.

Все свойства веществ можно разделить на физические (плотность, удельный вес, вязкость, поверхностное натяжение и др.) и теплофизические (удельная теплоемкость, теплопроводность, температуропроводность и др.). Данные об этих свойствах для различных веществ и растворов в зависимости от температуры и давления приводятся в справочниках.

Рассмотрим основные свойства веществ.

Плотность. Отношение массы тела (вещества) к его объему называют плотностью. Плотность (кг/м³)

p = М/V,

где М— масса тела, кг; V— его объем, м³.

Плотность представляет собой величину, обратную удельному объему у_уд, т. е. объему, занимаемому единицей массы вещества; ρ = 1/v_уд, где v_уд = V/М.

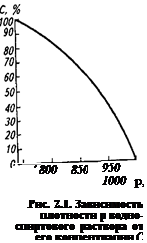
Плотность раствора зависит от его массовой доли С (рис. 2.1).

Отношение плотностей двух веществ называют относительной плотностью. Обычно относительную плотность веществ определяют относительно плотности дистил­лированной воды:

ρ_отн = ρ/ρ_в,

где ρ — плотность вещества; ρ_в — плотность воды.

Плотность суспензии (кг/м³)

ρ_с = ρ_твφ + ρ_ж(1 - φ),

где ρ_тв -плотность твердых частиц в суспензии, кг/м³; φ — доля твердой фазы в суспензии; р_ж — плотность жидкости, кг/м³.

Плотность сахарных сиропов, фруктовых соков, молока с сахаром при 20 °С находят по формуле

ρ ₂₀=10[1,42х + (100-х)],

где х — концентрация сухих веществ, %

При температурах, отличных от 20 °С, используют формулу

ρ_t= ρ₂₀ – 0,5(г-20),

где t - температура продукта, ⁰С.

Плотность томатопродуктов

р= 1016,76 + 4,4х - 0,53/.

Для характеристики сыпучих продуктов (зерна, сахарного песка, картофельной крупки и т. д.) вводят понятие насыпной плотности:

ρ_Н = (1 – ε) ρ_тв

где ρ_Н — насыпная плотность сыпучего продукта, кг/м³; ε — порозность (пористость) сыпучего материала; ε = Vм/ Vн; Vм — объем пустот свободно насыпанного материала, м³; V_H — объем свободно насыпанного материала, м; ρ_тв —действительная плотность частиц материала, кг/м³.

Для свободно насыпанных материалов порозность обычно находится в пределах ε = 0,38.-0,42.

Плотность газов (кг/м³) вычисляют по формуле Клапейрона:

ρ = ρ₀*Т₀р/Тр₀ = М(273р)/22,4(Тр₀)

где ρ₀= М/22,4 - плотность газа при нормальных условиях (Т_о – 273 К; р₀ = 1013 кПа), кг/м³; М-молекулярная масса газа, кг/моль, Т— абсолютная температура, К.

Плотность смеси газов

p_см= n₁ρ₁ + n₂ρ + n₃ρ + ……,

где n₁, n₂, n₃ — объемные доли компонентов газовой смеси; р₁, р₂, р₃ — соответствующие плотности компонентов.

Отношение веса тела к объему называют удельным весом и обозначают через Y:

Υ=G/V

В системе единиц СИ удельный вес измеряется в ньютонах на кубический метр. Масса и вес связаны между собой соотношением

G=mg,

где g — ускорение свободного падения, м/с².

Отсюда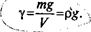

Вязкость. Вязкостью называют свойство жидкости оказывать сопротивление силам, вызывающим относительное перемещение ее частиц при ламинарном течении. Различают динамическую и кинематическую вязкость.

Причиной вязкостного сопротивления движению является молекулярное взаимодействие между частицами жидкости, а также взаимодействие между молекулами жидкости и движущегося в ней твердого тела.

Вязкостью обусловлена сила внутреннего трения, которая направлена в сторону, противоположную движению слоя, перемещающегося с большей скоростью, и действует на этот слой. Тем самым сила внутреннего трения вызывает сопротивление движению этого слоя жидкости.

Вязкость является основным отличием реальной жидкости от идеальной, которая вязкости не имеет.

Первоначальные основы закона внутреннего трения между слоями жидкости даны Ньютоном в 1686 г. и сводятся, в частности, к следующему:

1). вязкость и сила внутреннего трения практически не зависят от давления;

2). сила внутреннего трения прямо пропорциональна относительной скорости перемещения смежных слоев, или градиенту скорости. Под относительной скоростью в данном случае понимают приращение скорости при переходе от одного слоя (а) к другому (В) по нормали к направлению движения жидкости, т. е. dw/dn (рис. 2.2). Это приращение скорости на единицу длины по нормали к движению потока называют градиентом скорости.

Всесторонние исследования распределения скорости по нормали к стенке показали, что скорость струек различна. По мере приближения исследуемого потока к стенке скорость его уменьшается. На самой поверхности стенки жидкость как бы прилипает к ней, и скорость становится равной нулю. И наоборот, по мере удаления струйки от стенки скорость ее увеличивается. В дальнейшем высказанное Ньютоном положение о внутреннем трении жидкости было проверено опытами крупнейшего русого ученого Н. П. Петрова (1836-1920).

Математическая формулировка закона Ньютона:

Т= μFdw/dn,

где Т — сила внутреннего трения или касательная сила, которую нужно прилагать, чтобы перемещать один слой жидкости относительно другого с постоянной скоростью, Н; μ - динамический коэффициент вязкости или динамическая вязкость (Па с); F - площадь соприкосновения слоев жидкости, м²; dw/dn — градиент скорости (1/с).

В технической системе единиц динамическая вязкость измерения в пуазах (П) или сантипуазах и связана с единицей динамикой вязкости в системе СИ выражением: 1 П = 10^-5 Па • с.

Из закона Ньютона вытекает понятие об удельной силе внутреннего трения, или касательном напряжении

ǐ = T/F= μdw/dn.

Из последнего выражения следует, что при dw/dn=1 ǐ= μ. Следовательно, коэффициент динамической вязкости выражает силу трения Т, приходящуюся на единицу площади поверхности F между двумя скользящими один относительно другого слоями, когда на единице длины нормали к поверхности скольжения скорость движения изменяется на единицу скорости.

Кинематическая вязкость (м²/с) определяется по следующему уравнению:

υ=μ/ρ

В технической системе единиц кинематическая вязкость измеряется в стоксах (Ст) или сантистоксах. Соотношение единиц киматической вязкости в технической системе единиц и в системе СИ имеет вид: 1 Ст = 10^-4 м²/с = 1 см²/с = 1см²/с

Эталоном вязкости служит дистиллированная вода, поэтому иногда вязкость измеряют в градусах Энглера. Вязкость в градусах Энглера (⁰Е) является отношением времени истечения 200 см³ исследуемой жидкости из некоего сосуда ко времени т. истечения того же объема дистиллированной воды из того же сосуда при температуре 20⁰С, т. е. °Е = ǐ₁/ǐ.

Переход от вязкости в градусах Энглера к кинематической вязкости в системе СИ (см²/с) выполняется по эмпирической формуле Убеллоде

V = 0,0731 * ⁰Е – 0,0631/⁰Е

Вязкость капельных жидкостей значительно снижается с возрастанием температуры. Вязкость газов, наоборот, увеличивается с ее повышением. Причина различия влияния температуры на вязкость капельных жидкостей и газов обусловлена тем, что вязкость газов имеет молекулярно-кинетическую природу, а вязкость капельных жидкостей зависит в основном от сил сцепления между молекулами. Поскольку плотность газов примерно в тысячу раз меньше плотности капельных жидкостей, то их кинетическая вязкость может быть больше вязкости этих жидкостей.

Теплоемкость.Это отношение количества теплоты, подводимой к веществу, к соответствующему изменению его температуры. Теплоемкость единицы количества вещества с называют удельной теплоемкостью. В расчетах используют массовую, объемную и мольную удельные теплоемкости.

Удельная теплоемкость зависит от того, при каком процессе (изобарном, изохорном, адиабатном, политропическом, изотермическом) происходит обмен энергией между веществом и окружающей средой.

Наиболее часто в расчетной практике используют удельные изобарную теплоемкость с_р и изохорную теплоемкость c_v, которые связаны между собой уравнением c_p — с_y=R, где R — универсальная газовая постоянная, Дж/(моль • К); Дж/(кг • К).

Отношение с_р/с_у = к называют показателем адиабаты.

Массовая удельная теплоемкость показывает, какое количество теплоты надо сообщить веществу массой 1 кг, чтобы повысить его температуру на один градус.

Теплоемкость жидкостей и газов зависит от температуры и уве­личивается с повышением ее. Экспериментальные значения удель­ных теплоемкостей пищевых продуктов приводятся в соответству­ющих справочниках в виде таблиц и эмпирических формул.

Удельные теплоемкости жидкостей изменяются в диапазоне от 0,8 до 4,19 кДж/(кг • К), газов — от 0,5 до 2,2, твердых веществ — от 0,13 до 1,8кДж/(кгК).

Удельная теплоемкость неоднородных систем

C_р=с_αφ_α + с_bφ_b + с_сφ_с

где с_α, с_b, с_с — массовые удельные теплоемкости компонентов; φ_α, φ_b, φ_с — массовые доли соответствующих веществ в смеси.

Удельная теплоемкость томатопродуктов [Дж/(кт • К)]

с = 4228,7 -20,9х-10,88t

где х —концентрация сухих веществ; t — температура, ⁰С;

растительного сырья

с = с_с(1 -0,01w) + 41,87w,

где с_с _ удельная теплоемкость сухих веществ; w — влажность, %.

Удельная теплоемкость сахарозы

с = 4190 - 0,01x• 2510 - 7,54t+ 4,61(100 -Дб),

где Дб —доброкачественность продукта, %;

теста

с= 1675(1 + 0,015w);

зерна

с = 1550 + 26,4w.

Теплопроводность. Теплопроводностью называют процесс переноса энергии от более нагретых участков тела к менее нагретым в результате теплового движения и взаимодействия микрочастиц, приводящий к выравниванию температуры тела.

Интенсивность теплопроводности в твердых материалах, жидкостях и газах характеризуется коэффициентом теплопроводности λ, который является физическим свойством (теплофизическим параметром) вещества и показывает, какое количество теплоты проходит через 1 м² поверхности в течение единицы времени при Градиенте изменения температур в направлении, перпендикулярном изотермической поверхности, равном 1. Иногда λ называют теплопроводностью.

Коэффициент теплопроводности жидкости при температуре около 30 °С можно рассчитать по формуле

λ₃₀=A₁cр³р/М

где А₁ — коэффициент, зависящий от степени ассоциации жидкости (для ассоциированных жидкостей, например воды, А₁ = 3,58* 10^-8 для неассоциированных жидкостей, например бензола, А₁ = 4,22 • 10^-8); с - удельная теплоемкость жидко­сти, Дж/(кг • К); р — плотность жидкости, кг/м3; М— молекулярная масса.