Зависимость между главными моментами системы сил относительно двух центров приведения.

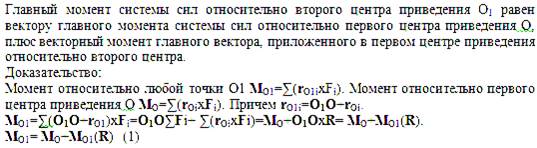
44) Инварианты системы сил. Частные случаи приведения.

Инварианты в статике, такие величины, для рассматриваемой системы сил, которые не изменяются при изменении центра приведения.

Виды инвариантов:

1) Векторный инвариант - главный вектор системы сил (R);

2) Скалярный инвариант.

L0 * R = L01 * R

L01 = L0 + O1O * R

L01 * R = L0 * R + (O1O * R) * R = L0*R + (R * R) * O1O

L01 * R = L0 * R

Скалярное произведение главного вектора на главный момент не зависит от центра приведения.

L01 * R * cosα = L0 * R * cosα

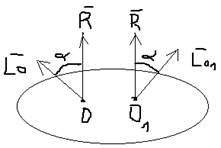
L01 * cosα = L0 * cosα

Проекция главного момента на шлавный вектор не зависит от центра приведения.

Частные случаи приведения системы сил:

1) Приведение к паре сил.

В этом случае система сил приводится к одной паре.

R0 = R = 0

L01 = L0 + O1O * R

2) Приведение к равнодействующей.

а) Если L0 = 0, то R = R*.

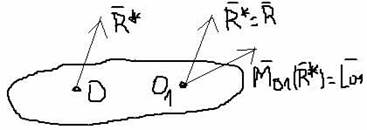
Линия действия проходит через центр приведения.

б) Если R≠0 , L0≠0, но R перпендикулярен L0.

OY перпендикулярен (L0,R)

d= L0 / R = OO1

| M01(R) | = d * R = L0

Отбросим (L,M0(R)), т.к. ~0 и останется R*.

Плоская система сил всегда может быть приведена к равнодействующей.

3) Приведение к динамическому винту (к динаме).

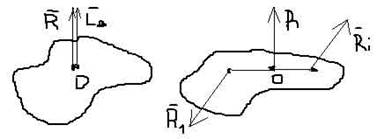
Динамический винт - такая совокупность главного момента и главного вектора, когда векторы параллельны.

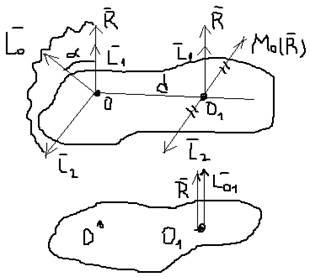
L0 = L1 + L2

|L1| = L0 * cosα

L2 = L0 * sinα

d = L2 / R

M01(R) = O1O * R

L0 * R = L0 * R * cosα = LxRx + LyRy + LzRz

L0 = Lxi + Lyj + Lzk

R = Rxi + Ryj + Rzk

cosα = (RxLx + RyLy + RzLz)/(L0*R)

(Другой вариант ответа)