Условия равновесия произвольной системы сил. Частные случаи.

Произвольная система сил, приложенных к твердому телу, эквивалентна силе, равной главному вектору R, и паре сил с моментом, равным главному моменту L0 относительно какого-либо центра О. Чтобы такая система находилась в равновесии, необходимо и достаточно равенство нулю и главного вектора R, и главного момента L0. Поэтому условия равновесия пространственной системы сил могут быть представлены в векторной форме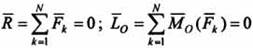
Два векторных условия эквивалентны следующим шести аналитическим условиям равновесия:

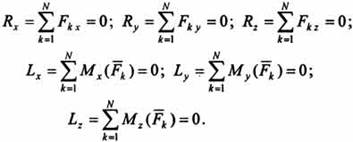
Условия равновесияможно сформулировать так: для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на оси декартовой системы координат равнялись нулю и суммы моментов всех сил относительно этих осей также равнялись нулю.

Частные случаи.

Условия равновесия пространственной системы параллельных сил.

Если силы, действующие на твердое тело, параллельны между собой, то можно выбрать такую систему координат, когда одна из ее осей, например Oz, параллельна направлению действия сил (рис.). Тогда из шести аналитических условий равновесия три выполняются тождественно, и система параллельных сил будет иметь только три условия равновесия:

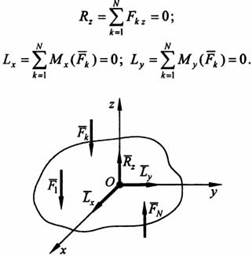
Условия равновесия плоской системы сил.Для плоской системы сил условия равновесия будут частным
случаем уравнений , 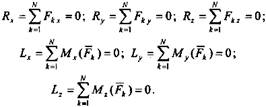определяющих условия равновесия пространственной системы сил. Например, если силы расположены в плоскости Оху, то аналитические условия равновесия можно записать в виде: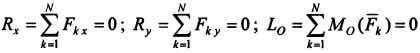
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма алгебраических моментов этих сил относительно любого центра О были равны нулю. Алгебраическим моментом силы относительно точки называют момент силы относительно оси, проходящей через данную точку перпендикулярно плоскости, в которой расположена сила и
точка.
Вместо 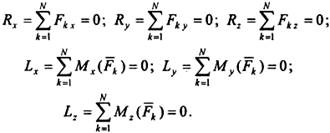иногда удобно применить условия равновесия в виде уравнений трех моментов: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех этих сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю: .

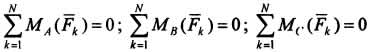Необходимость утверждения следует из того, что третье условие 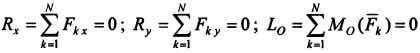справедливо для любой точки. Достаточность докажем методом от противного, используя теорему о приведении произвольной системы сил к центру. Допустим, что плоская система сил не находится в равновесии. Тогда, приводя ее поочередно к точкам А, В, С, будем иметь в этих точках равнодействующую R . Для выполнения равенств 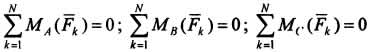равнодействующая должна пройти одновременно через все три точки, а это невозможно, так как точки не лежат на одной прямой. Следовательно, равнодействующая равна нулю и система сил, удовлетворяющая
равенствам 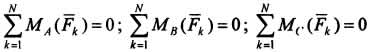, находится в равновесии.