Функциональные последовательности
Если членами ряда будут не числа, а функции от х, то ряд называется функциональным.
Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится.
Совокупность таких значений называется областью сходимости.
Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:
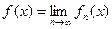
Последовательность {fn(x)} сходится к функции f(x) на отрезке [a,b], если для любого числа e>0 и любой точки х из рассматриваемого отрезка существует номер N = N(e, x), такой, что неравенство
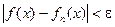
выполняется при n>N.
При выбранном значении e>0 каждой точке отрезка [a,b] соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка [a,b], будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка [a,b], т.е. будет общим для всех точек.
Последовательность {fn(x)} равномерно сходится к функции f(x) на отрезке [a,b], если для любого числа e>0 существует номер N = N(e), такой, что неравенство
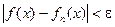
выполняется при n>N для всех точек отрезка [a,b].
Пример. Рассмотрим последовательность 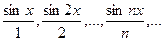
Данная последовательность сходится на всей числовой оси к функции f(x)=0, т.к.
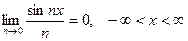
Дата добавления: 2020-06-09; просмотров: 533;











