Интегральный признак Коши

Пусть дан ряд 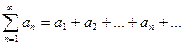с положительным членами, причем 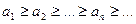и f(x) – такая непрерывная монотонно убывающая функция, что f(п)=а_п. тогда данный ряд и несобственный интеграл 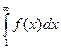одновременно сходятся или расходятся.

Пример. Ряд 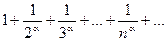сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл 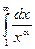сходится при a>1 и расходится a£1. Ряд 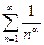называется обобщенным гармоническимрядом.

Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными.

Знакочередующиеся ряды

Ряд называется знакочередующимся, если положительные и отрицательные члены следуют друг за другом поочередно.

Знакочередующийся ряд можно записать в виде:

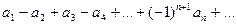, где

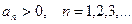
Признак Лейбница

Если у знакочередующегося ряда 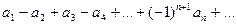абсолютные величины u_i убывают 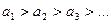и общий член стремится к нулю 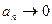, то ряд сходится. При этом сумма S ряда удовлетворяет неравенствам: 0 < S < u_n.

Теорема. Пусть даны знакопеременный ряд (с членами произвольных знаков).

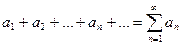(1)

и ряд, составленный из абсолютных величин членов ряда (1):

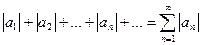(2)

Тогда из сходимости ряда (2) следует сходимость ряда (1).