Необходимые условия сходимости ряда

1) Если ряд 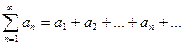сходится, то общий член ряда а_n стремится к нулю (т.е. 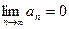). Однако, это условие не является достаточным. Например, гармонический ряд 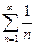является расходящимся, хотя его общий член и стремится к нулю.

Если 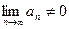, то ряд расходится.

Пример. Исследовать сходимость ряда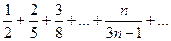

Найдем 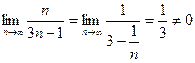- необходимый признак сходимости не выполняется, значит ряд расходится.

2) Если ряд (1) сходится, то последовательность его частных сумм ограничена.

Однако этот признак также не является достаточным.

Например, ряд 1 – 1 + 1 – 1 + 1 – 1 + … + (-1)ⁿ⁺¹ +… расходится, т.к. расходится последовательность его частных сумм в силу того, что

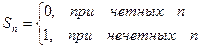
При этом последовательность частных сумм ограничена, т.к. 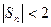при любом n.

Ряды с неотрицательными членами

При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.

Теорема. Для сходимости ряда 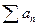с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.