Асимптоты графика функции

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.

Асимптотой кривой называется прямая, к которой неограниченно приближается график функции.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

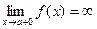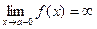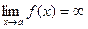Вертикальные асимптоты. Если , , или , то прямая х = а является вертикальной асимптотой кривой y = f(x). Вертикальные асимптоты обычно сопровождают точки разрыва второго рода и если функция непрерывна, то вертикальных асимптот нет.

Например, для функции 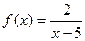прямая х = 5 является вертикальной асимптотой.

Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.

Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.

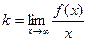
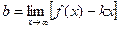
Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.

Пример. Найти асимптоты и построить график функции .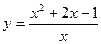

1) Вертикальные асимптоты: y®+¥при x®0-0, y®-¥ при x®0+0, следовательно, прямая х = 0 является вертикальной асимптотой.

2) Наклонные асимптоты:

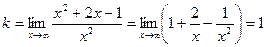
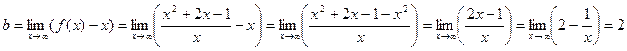
Таким образом, прямая у = х + 2 является наклонной асимптотой.

Пример. Найти асимптоты и построить график функции .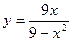

Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.

Найдем наклонные асимптоты: ,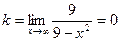

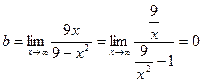
Следовательно, y = 0 – горизонтальная асимптота.