Температурное поле в твердом теле

Энергию частиц вещества в твердых в телах характеризует температура.

Совокупность температур в денный момент времени для всех точек твердого тела называют температурным полем.

В общем случае температура в любой точке твердого тела зависит от координат точки и времени

Q = f₃ (x, y, z, t ), (1.1)

где x,y,z – координаты точки,

t – время.

Эта формула выражает трехмерное температурное поле. На практике встречаются случаи, когда изменение температуры по одной или двум координатам незначительно и им можно пренебречь.

Например, если изменение температуры по координате z незначительно, то

,

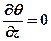формула(1.1) имеет вид

Q = f₂ (x,y, t ) (1.2)

и описывает двумерное температурное поле.

Аналогично, если изменение температуры по координатам z и y незначительно, то 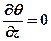, 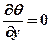и

Q = f₁ (x, t ), (1.3)

Формула (1.3) описывает одномерное температурное поле.

Если температура точек тела изменяется во времени, то температурное поле называется нестационарным, а тепловой режим неустановившимся.

Если температура точек тела не меняется во времени, т.е. 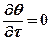, то поле называется стационарным, а тепловой режим – установившимся.

Для стационарного температурного поля и установившегося режима имеем

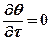и Θ = f₃ (x, y, z), (1.4)

Θ = f₂ (x, y), (1.5)

Θ = f₁ (x), (1.6)

Формулы(1.4, 1.5, 1.6) описывают трехмерное, двумерное и одномерное стационарные температурные поля.

Если соединить все точки тела, имеющие одинаковую температуру, то получим изотермическую поверхность. Любая линия на этой поверхности является изотермой. Изотермические поверхности не могут пересекаться или иметь общие точки.

При переходе с одной изотермической поверхности на другую наблюдается изменение температуры.

Рассмотрим семейство изотерм, отличающихся друг от друга значениями температур на величину ΔΘ (рис. 1.1)

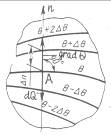
Рис. 1.1 – Семейство изотерм на плоскости

Скорость изменения температуры в точке А тела при переходе от одной изотермы к другой будет максимальной вдоль нормали (n). Эта скорость определяется отношением ΔΘ/Δn.

Скорость изменения температуры характеризуется градиентом температуры.

Градиентом температуры называется вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры. Он численно равен

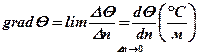(1.7)

и изображен на рис 1.1

Градиент температуры характеризует интенсивность изменения температуры внутри тела.