Выбор оптимального распределения надежности отдельных элементов КСНО

Обычно стоимость отдельного элемента КСНО может быть представлена в виде зависимости

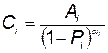, (5.90)

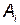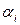где и ; — коэффициенты, позволяющие статистические данные аппроксимировать кривой; 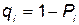— вероятность отказа i-го элемента.

Вероятность безотказной работы КСНО при отсутствии резервирования может быть определена по формуле (для случая малых значений)

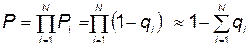. (5.91)

Отсюда

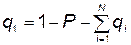.(5.92)

Суммарная стоимость КСНО складывается из стоимостей отдельных элементов:

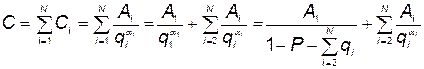. (5.93)

Следует выбрать вероятность отказа i-го элемента 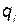таким образом, чтобы суммарная стоимость КСНО была минимальной. Для этого необходимым условием является равенство нулю всех частных производных от С по :

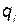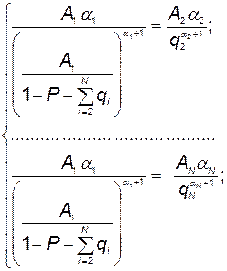(5.94)

т. е.

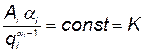. (5.95)

Из (5.95) имеем

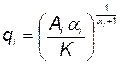. (5.96)

Подставив 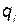вычисленное по формуле (5.96), в формулу (5.91), будем иметь

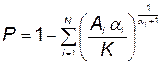. (5.97)

Откуда при 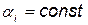можно определить

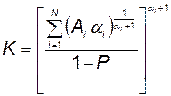. (5.98)

Выражение (5.96) с учетом (5.98) можно записать

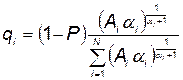. (5.99)

Полученная зависимость дает возможность найти оптимальное распределение надежности отдельных элементов при заданной надежности всего КСНО (или агрегата КСНО), а также совместно с уравнением (5.93) позволяет найти зависимость 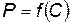при оптимальном распределении надежности отдельных элементов. Имея зависимость 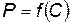и пользуясь методикой для выбора оптимальной надежности КСНО или его агрегатов, изложенной выше, можно определить оптимальную надежность всего КСНО.

Следует отметить, что выбор оптимального режима тренировок элементов КСНО, а также оптимального времени замены этих элементов может производиться независимо от выбора общей надежности всего комплекса или его отдельного агрегата.

5.4.5. Определение оптимального числа резервных элементов КСНО

Как указывалось выше, одним из эффективных методов повышения надежности КСНО является резервирование его элементов. В свою очередь, увеличение количества элементов приводит к увеличению весовых характеристик и габаритных размеров, а также стоимости всего КСНО.

Если надежность всего КСНО задана, то при наличии резервирования вероятность безотказной работы будет

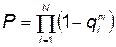, (5.100)

где 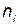— количество i-x элементов повышающих надежность за счет резервирования; 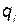— вероятность отказа i-го элемента; 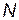- общее количество разнотипных элементов (дублирующие элементы не входят).

Определение оптимального числа резервных элементов 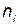заключается в выборе такого вектора 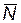(с компонентами 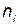), который минимизирует суммарную стоимость КСНО.

Суммарная стоимость КСНО может быть представлена следующей зависимостью:

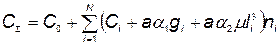, (5.101)

где 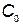— постоянная составляющая затрат, не зависящая от резервирования; 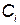, а — статистические коэффициенты; 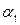, 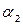— коэффициенты, учитывающие увеличение массы 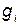и размеров 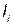за счет введения дополнительных элементов; 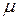— коэффициент, учитывающий увеличение объема за счет размеров .

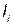При определении оптимального количества резервных элементов следует учитывать возможность существования ограничений по массе и габаритам, которые для данного случая могут быть представлены в следующем виде:

;

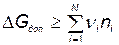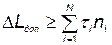; (5.102)

где ; .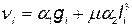

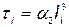Поставленная задача формулируется так: необходимо выбрать вектор 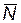с компонентами 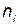таким образом, чтобы при соблюдении условия (5.100) и ограничений (5.102) минимизировать 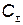, определяемую по формуле (5.101).

В общем случае эта задача нелинейного целочисленного программирования, которая при больших значениях может быть решена либо методом полного перебора, либо наискорейшего спуска, либо другими численными методами с применением ЭВМ.

В простейшем случае, когда 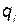малы и отсутствуют ограничения по массе и габаритам, поставленная задача может быть решена аналитически.

Для этого случая можно записать приближенное уравнение, получаемое из (5.100):

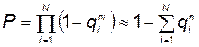. (5.103)

Уравнение (5.101) перепишем в виде

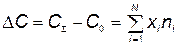, (5.104)

где .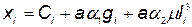

Оптимизацию будем проводить методом неопределенных множителей Лагранжа, для чего составим функцию

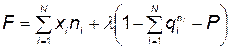(5.105)

и, приравняв производные по 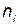и 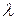кнулю, получим

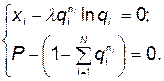(5.106)

Решение этой системы уравнений позволяет найти оптимальное значение

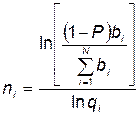, (5.107)

где .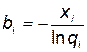

Вместо натуральных логарифмов в приближенных расчетах можно пользоваться десятичными.