Обоснование необходимой численности операторов и распределение функций между ними

Для решения задачи обоснования потребной численности операторов и распределения функций между ними необходимы следующие исходные данные:

-множество иерархических уровней управления ( 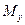), которое определяет минимальное количество операторов ( );

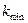-множество типов задач управления ( 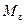), которые должны решать операторы;

-опорный вариант распределения функций между операторами, который определяется множествами 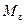и ;

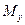-множество типов уровней приоритетов ( 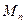) задач;

-множество недопустимых перераспределений функций, определяемое множествам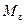и и ;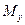

-временные ( 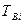) и надежностные ( 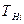) характеристики решения задач управления операторами ( 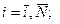N - мощность множества ) .

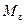Исходные данные характеризуют опорную организационную структуру коллектива операторов, описываемую матрицей сопряжения 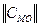. Элементы матрицы сопряжения могут быть определены следующим образом:

,

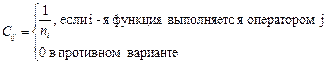где n_i - количество операторов, выполняющих частями последовательно i-ю задачу.

Организационная структура (рациональная матрица сопряжения 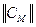) определяется в классе допустимых матриц сопряжения 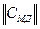. При определении организационной структуры должны использоваться следующие критерии:

-минимизации количества операторов k;

-максимизации вероятности (P) безошибочного и своевременного выполнения коллективом операторов всего комплекса задач управления в соответствии с типовым вариантом функционирования системы управления;

-обеспечения ограничений на показатель загруженности k_з по каждому оператору;

-минимизации показателя равномерности загрузки k_p между операторами одного уровня;

-минимизации общей стоимости содержания организационной структуры.

Показатель k в силу его прямо пропорциональной зависимости от стоимостных показателей системы управления является основной эргономической характеристикой и определяется простой дискретной функцией, ограниченной снизу и сверху:

.

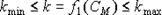Для расчета второго показателя с учетом специфики системы управления целесообразно построение статистической имитационной модели групповой деятельности с использованием принципов и методов теории массового обслуживания. При расчете P с использованием модели необходимы дополнительные данные: плотностей возникновения задач управления 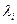и законов распределения времени существования задач 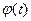. Эти данные определяют на основе анализа типового варианта функционирования системы управления. В соответствии с эргономическим требованиями к организации системы управления P ограничен снизу P_min и рассчитывается с использованием неявно заданного (в виде статистической имитационной модели) функционала:

.

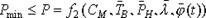Показатель P в силу его прямой корреляции с показателями эффективности системы управления также является основной эргономической характеристикой организационной структуры .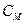

Показатели загруженности k_з, равномерности загрузки k_р взаимосвязаны с показателем Р и являются вспомогательными. Поэтому при постановке задачи они должны учитываться при формировании ограничений.

Показатель стоимости S зависит от затрат 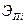на подготовку и содержание оператора i-го иерархического уровня и затрат 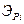на производство и эксплуатацию рабочего места:

,

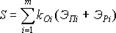где k_Oi - количество операторов i-го иерархического уровня;

m - количество иерархических уровней.

Ограничения по стоимости также необходимо учитывать при постановке задачи.

С учетом анализа критериев задача может быть поставлена следующим образом [18].

Определить структуру C_M, при которо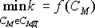й

и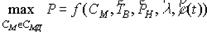

и выполняются ограничения на основные критериальные функции

,

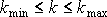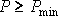
и вспомогательные критерии

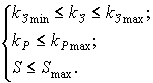
Поставленная задача является задачей двухпараметрического векторного синтеза, которая обладает специфической особенностью, заключающейся в том, что первый критерий принимает небольшое конечное число значений. Поэтому она может быть решена методом рабочих характеристик. Метод заключается в построении рабочей характеристики:

.

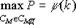При этом максимизация по второму критерию осуществляется для всех допустимых значений первого:

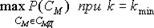и ограничениях;

................................................................

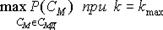и ограничениях.

Построенная таким образом рабочая характеристика представляет собой монотонно возрастающую функцию. Векторная задача синтеза не будет иметь решения только в том случае, если рабочая характеристика не будет пересекать область строго допустимых структур.