Показатели безотказности

Безотказность – вероятность того, что в пределах заданной наработки отказа объекта не возникнет.

Показатели безотказности невосстанавливаемых объектов:

- вероятность безотказной работы Р(t₀) – вероятность того, что в пределах заданной наработки отказ объекта не возникнет;

- интенсивность отказов l(t)– условная плотность возникновения отказа, определяемая для рассматриваемого момента времени при условии, что до этого отказ не возник;

- средняя частота отказоw(t);

- средняя наработка до отказа T₀ – математическое ожидание наработки до первого отказа;

- наработка на отказ Т – среднее время между соседними отказами для восстанавливаемых изделий.

Математическое определение вероятности безотказной работы от начала эксплуатации до t₀ (рис.2.1):

- вероятностное

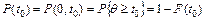, (2.1)

где 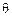– случайное время работы (наработки) объекта до отказа (между отказами);

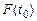– функция распределения случайной величины ;

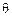- статистическое

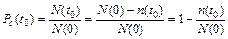, (2.2)

где 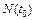– количество исправленных объектов в момент времени t₀;

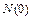– количество исправленных объектов в момент времени t = 0; 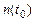– количество отказов объектов за время t₀.

Рассмотрим это на примере:

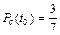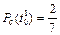; или ; ;

; ; .

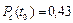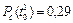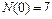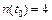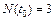Если отсчет времени работы производится от произвольного момента t, то вероятность безотказной работы в интервале времени от t до t + t₀ может быть определена на основании теоремы умножения вероятностей.

Действительно,

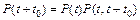. (2.3)

вероятностный способ определения:

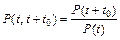, (2.4)

где 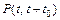– вероятность того, что объект проработает безотказно в течение заданного времени t₀, начиная с момента времени t, или условная вероятность того, что случайное время работы до отказа окажется больше t + t₀ при условии, что объект уже проработал безотказно до момента времени t.

Статистический способ определения:

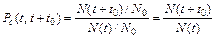, (2.5)

где 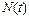– количество объектов, исправленных к моменту времени t.

Рис.2.1. Определение безотказности: а – вероятностное;

б – статистическое

Пример. На угольном разрезе при эксплуатации из 10 участковых насосов в течение года отказали 3.Определить вероятность безотказной работы за год.

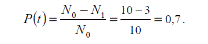
Таким образом, 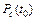– отношение числа объектов, безотказно проработавших до момента времени t₀, к числу объектов, исправленных в начальный момент времени t = 0, или частость события, состоящего в том, что реализация времени работы объекта до отказа окажется больше заданного времени работы t₀.

При вероятности отказа в интервале времени от 0 до t₀:

- вероятностное определение :

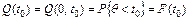, (2.6)

где Q(t₀) – вероятность того, что объект откажет в течение заданного времени t₀, начав работу при t = 0, или того, что случайное время работы объекта до отказа окажется меньше заданного времени t₀; очевидно, что Q(t₀) = 1 – Р(t₀), так как события несовместны;

- статистическое определение

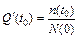. (2.7)

При вероятности отказа в интервале времени от t до t + t₀:

- вероятностное определение:

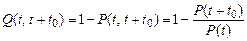- ; (2.8)

- статистическое определение:

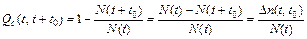, (2.9)

где Dn(t, t₀) – число общих отказов именно в интервале времени (t, t + t₀).

Плотность распределения отказов объекта расчитывается:

- вероятностное определение:

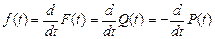, (2.10)

где f(t) – плотность вероятности того, что время работы объекта до отказа меньше t, или плотность вероятности отказа к моменту времени t;

- статистическое определение:

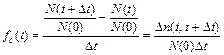. (2.11)

На практике необходимо, чтобы Dt было достаточно мало, а Dn(t, t + Dt) достаточно велико, т.е. необходимо проводить испытания большого числа объектов; 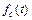– частость отказов в интервале времени (t, t + Dt), или отношение числа отказов в интервале времени (t, t + Dt) к произведению числа исправных объектов в начальный момент времени t = 0 на длительность интервала времени Dt.

Для интенсивности отказов :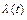

- вероятностное определение. Из определения интенсивности отказов по теореме умножения вероятностей имеем:

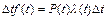(2.12)

или

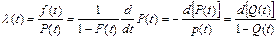, (2.13)

где f(t) – плотность вероятности отказа объекта к моменту времени t при условии, что до этого момента отказ изделия не произошел;

- статистическое определение:

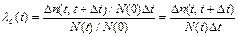, (2.14)

где Dn – велико;

Dt – мало;

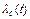– отношение числа отказов в интервале времени (t, t + Dt) к произведению числа исправленных объектов в момент времени t на длительном интервале времени Dt (количество отказов одного объекта в единицу времени при условии, что до этого момента отказ изделия не произошел).

На практике при установлении статистического значения 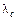(t) пользуются формулой

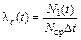(2.15)

где 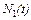– число отказавших изделий в интервале времени ;

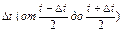N_ср– среднее число исправно работавших изделий в интервале .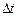

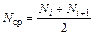(2.16)

где N_i, N_i+1 – число исправно работающих изделий соответственно в начале и конце интервала .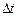

Пример. При эксплуатации 20 экскаваторов в течение 3 лет произошло 15 отказов электропривода подъема. Определить интенсивность отказов в течение периода эксплуатации.

.

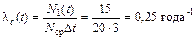Время средней наработки до отказа:

- вероятностное определение для непрерывной наработки:

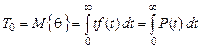, (2.17)

где Т₀ – математическое ожидание наработки до первого отказа;

- статистическое определение:

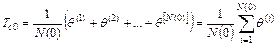, (2.18)

где 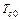– среднее арифметическое реализации времени работы объекта до отказа.

На практике при расчете Т₀ по результатам наблюдения статистический показатель 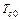_. определяют по формуле

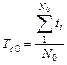, (2.19)

где N₀–число элементов под наблюдением;

t_i – время безотказной работы i -го элемента.

Пример. При наблюдении за работой 10 экскаваторов было установлено следующее время наработки до отказа: 200; 350; 280; 400; 450; 360; 380; 430; 260 и 150 часов. Определить среднюю наработку на отказ экскаваторов.

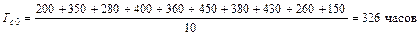
Если известна одна из функций 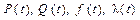, то через нее можно определить остальные (табл.2.1).

Таблица 2.1