Функциональная связь между показателями надежности

Извест- ная функция	Формулы для определения трех остальных функций
P(t)	Q(t)	f(t)	l(t)
P(t)	–	1 – P(t)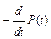
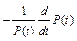
Q(t)	1 – Q(t)	–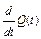
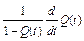
f(t)			–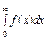
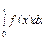
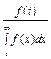
l(t)				–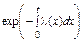

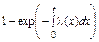
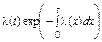
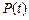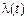Найдем зависимость от . Из определения плотности отказов и интенсивности отказов имеем:

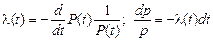; (2.20)

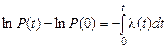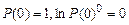, , (2.21)

следовательно,

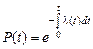. (2.22)

Определение показателей безотказности для восстанавливаемых объектов выполняется так же, как и для невосстанавливаемых объектов.

Вероятность безотказной работы Р^*(t) указывает на вероятность того, что в заданном интервале времени 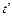или в пределах заданной наработки не возникнет отказ изделия.

Величина вероятности безотказной работы за некоторый промежуток времени может быть определена на основе статистических данных, характеризующих результаты испытаний элементов на надежность, как отношение числа элементов N(t), оставшихся исправными в конце рассматриваемого интервала времени t, к начальному числу испытываемых элементов N(t₀):

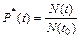. (2.23)

При значительном числе испытываемых элементов статистическая вероятность Р*(t) сходится с вероятностью P(t), т.е. в пределе, равном истинному значению вероятности безотказной работы. Это отношение называется эмпирической функцией надежности.

Общими свойствами функции надежности для любых видов элементов являются следующие параметры: при t = 0 P(0) = 1, т.е. полагают, что в начальный момент времени элемент находится в исправном состоянии; P(t) является не возрастающей функцией времени, т.е. она либо монотонно убывает, либо на отдельных участках может оставаться постоянной; при 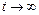, Р(t) 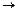0, т.е. при возрастающем времени работы элемента вероятность его безотказной работы уменьшается и стремится к нулю (рис. 2.2). Убывающая кривая полностью характеризует собой безопасность и долговечность неремонтируемых изделий. Наработка неремонтируемого изделия наступает при отказе и является его ресурсом. Различают ресурс до первого ремонта, межремонтный ресурс, средний ресурс.

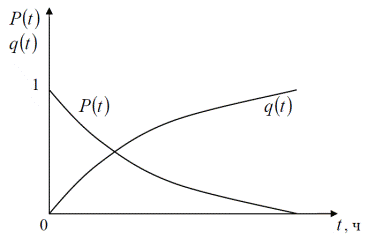
Рис. 2.2. Графики вероятности безотказной работы P(t)

и вероятности отказа q(t)

Показатели безотказности восстанавливаемых объектов:

- вероятность безотказной работы Р(t);

- параметр потока отказов w(t) – плотность вероятности возникновения отказа восстанавливаемого объекта, определяемая для рассматриваемого момента времени;

- наработка на отказ Т – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.

Вероятность безотказной работы определяется точно так же, как и для невосстанавливаемых объектов. Однако следует учитывать, что функции распределения наработки между началом эксплуатации и первым отказом, первым и вторым отказом и так далее, могут быть различными. Поэтому вероятность безотказной работы следует определять через соответствующую функцию распределения. При эксплуатации горного оборудования информацию о надежности собирают отдельно для новых и для вышедших из капитального ремонта объектов.

Моменты отказов формируют поток. Характеристикой потока отказов является ведущая функция W(t) – математическое ожидание числа отказов за время t:

W(t) = Мn(t). (2.24)

За интервал времени (t₁, t₂)

Мn(t₁, t₂) = W(t₂) – W(t₁). (2.25)

Функция

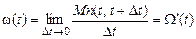. (2.26)

Параметр потока отказов есть среднее количество отказов в единицу времени. Иногда его называют средней частотой отказов.

Наработка на отказ определяется как отношение суммы наработки восстанавливаемых объектов к суммарному числу отказов этих объектов за некоторый период:

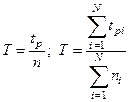, (2.27)

где N – число однотипных объектов.