Поглощение света. Фазовая и групповая скорость

1. Поглощение света. Из-за рассеяния энергии в резонаторах вещество поглощает свет. В результате световой поток по мере распространения света в веществе уменьшается. Найдем закон изменения светового потока с расстоянием в однородной поглощающей среде.

Пусть в направлении ОХ распространяется световой пучок постоянного сечения S. Обозначим S₀ эффективное сечение каждого поглощающего свет атома. Полагаем, что концентрация N₀ поглощающих атомов невелика, и атомы в выделенном объеме не затеняют друг друга.

Пусть световой поток Ф₀ входит в поглощающую среду в точке с координатой х (рис.185). После прохождения пучком бесконечно тонкого слоя толщиной dx часть энергии пучка поглотится. Количество поглощенной энергии dФ тем больше, чем больше поток Ф и чем больше отношение суммарного сечения поглощающих атомов в объеме Sdx к площади пучка S, то есть чем больше величина S₀∙N₀∙SdxçS. Отсюда 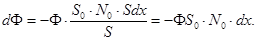(22.1)

Если принять, что после прохождения слоя dx энергетические “дверки” в пучке затягиваются за счет перераспределения потока энергии, то Ф – переменная величина. Разделяем переменные и интегрируем на отрезке l от х до x+l.

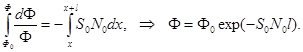(22.2)

Обычно суммарное эффективное сечение атомов в единице объема S₀N₀ называют коэффициентом поглощения среды, S₀N₀ = c. Тогда 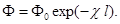Закон Бугера (22.3)

Световой поток в поглощающей среде убывает по экспоненциальному закону.

Формула (22.3) выражает закон Бугера. Пьер Бугер постулировал его на основе опытов в 1729 году. Если разделить формулу (22.3) на сечение пучка S, то получаем закон Бугера для интенсивности света. I = ФçS = I₀exp(–cl). (22.4)

Опытами доказано, что коэффициент поглощения c не зависит от интенсивности света в широких пределах, начиная от порога чувствительности человеческого глаза
I_min = 2.5∙10^–15 Вт/м² до интенсивности солнечных лучей в фокусе линзы I_max= 2∙10⁵ Вт/м². И лишь в лазерных пучках с ростом интенсивности c начинает уменьшаться.

2. Поглощение света в газах, жидкостях и твердых телах. В газах коэффициент поглощения c для большинства длин волн близок к нулю, и лишь в очень узких спектральных областях обнаруживает резкие максимумы, соответствующие резонансным частотам колебаний электронов в атомах или атомов в молекулах (рис.186).

Совокупность частот w ₀₁, w ₀₂… или соответствующих им длин волн l, при которых происходит поглощение света, называют спектром поглощения. В атомарных газах (инертные газы, пары металлов) спектры поглощения линейчатые (подробнее смотри §23).

В жидкостях наиболее важное практическое значение имеет поглощение света в растворах. Немец Бер в 1852 году показал, что в растворах с прозрачным растворителем и поглощающим свет растворенным веществом закон Бугера принимает вид: 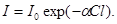Закон Бугера-Бера, 1852 (22.6)

Из закона Бугера – Бера следует, что коэффициент поглощения раствора c численно равный суммарной площади эффективного сечения поглощающих молекул в единице объема раствора, пропорционален концентрации раствора С, 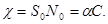(22.6)

Коэффициент a называют удельным показателем поглощения.

Зависимость поглощения света от концентрации поглощающих веществ используется для определения концентрации растворов. Метод измерения концентрации по поглощению света называется колориметрией (от лат. color – цвет), а приборы колориметрами. В отличие от газов спектры поглощения в жидкостях образуют широкие участки – полосы поглощения.

В твердых диэлектриках так же, как и в жидкостях, наблюдаются полосы поглощения. А в твердых и жидких металлах коэффициент поглощения охватывает очень широкий диапазон длин волн и примерно в миллион раз больше, чем у стекла. Это объясняется наличием в металлах свободных электронов, которые под действием электрического поля световой волны легко приходят в движение. В результате энергия электромагнитной волны переходит в энергию движения электронов и далее в энергию теплового движения узлов кристаллической решетки.

Так как концентрация свободных электронов в металлах очень велика (»10²² см^–3), то их вынужденные колебания порождают сильную отраженную волну. Ее интенсивность может достигать 90¸95 % падающей волны. В результате даже очень тонкие слои металла отражают большую часть падающего на них света, оставшуюся часть поглощают и поэтому практически непрозрачны.

Заметная прозрачность у металлов начинается при толщине пленки порядка длины волны l. Она увеличивается с уменьшением длины волны. Поэтому тонкие металлические пленки кажутся на просвет фиолетовыми.

3. Фазовая и групповая скорость света. В конце 19 века в связи с развитием лабораторных методов измерения скорости света встал вопрос об уточнении понятия скорости световой волны. Теоретически этот вопрос исследовал Рэлей. Он показал, что уравнение плоской монохроматической волны 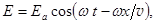(22.7)

используемое для наглядного описания интерференции, дифракции и других оптических явлений, представляет собой идеализацию, не реализующуюся в действительности. Ведь оно описывает математическую синусоиду, не имеющую в пространстве ни начала, ни конца.

В реальных же актах испускания, поглощения и прохождения света всегда существует локализация в пространстве и во времени светового импульса. Каждый атом испускает свет в течение конечного промежутка времени (»10^–8 с), поэтому реальный волновой цуг имеет в пространстве начало и конец. В общем случае он представляет собой апериодический процесс. Но благодаря тому, что длина отдельных элементарных цугов, испускаемых отдельными атомами, в миллионы раз превышает их длину волны, обрыв элементарных цугов сравнительно слабо влияет на их монохроматичность.

Наиболее ярко апериодичность колебаний вектора 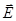проявляется в том случае, когда световой импульс формируется из нескольких элементарных цугов, испущенных разными атомами и имеющих разную длину волны.

На рис.187 показана общая форма светового импульса, состоящего из трех элементарных цугов с длинами волн l₁, l₂, l₃. Такой импульс, состоящий из набора гармонических волн, называется группой волн или волновым пакетом. Чем меньше частоты монохроматических волн, формирующих группу, отличаются между собой, тем более плавную форму имеет кривая, огибающая группу волн.

Каждая монохроматическая волна распространяется в пространстве с некоторой фазовой скоростью v, которая входит в уравнение монохроматической волны (22.7). Фазовая скорость есть скорость перемещения в пространстве определенной фазы монохроматической волны, например, гребня, узла или впадины. Величина фазовой скорости зависит от показателя преломления среды, v = с/n, где с – скорость света в вакууме.

Скорость перемещения энергии группы волн называется групповой скоростью. Иначе, групповая скорость – это скорость перемещения в пространстве светового импульса как целого.

4. Формула Рэлея. Найдем связь между групповой скоростью u светового импульса и фазовыми скоростями v составляющих его монохроматических волн. Для этого вычислим скорость u простейшей группы, образованной из двух монохроматических волн с одинаковыми амплитудами Е_а и близкими частотами w₁ и w₂.

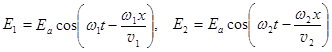, (22.8)

где 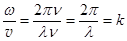называют волновым числом. (22.9)

Волны распространяются вдоль одной прямой ОХ, а векторы 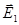и 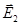колеблются в одной плоскости. Поэтому напряженность Е суммы двух волн есть: (21.10)

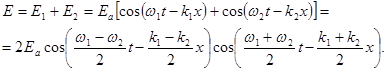Это известный из механики случай биений (рис.188).

Скорость u группы двух волн есть скорость перемещения огибающей 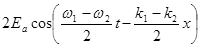. Она найдется из условия 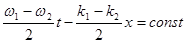- (22.11) постоянства фазы огибающей. Введем преобразования: w ₁=w ₀ + dw, w ₂=w ₀ – dw,

k₁ = k₀ + dk, k₂ = k₀ – dk. Здесь w ₀ = (w₁ + w ₂)ç2, k₀ = (k₁ + k₂)ç2.

Условие постоянства фазы огибающей принимает вид: 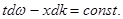(22.13)

Продифференцируем по времени t, приняв во внимание, что w и k – параметры волн, не зависящие от времен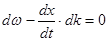и. , или 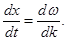(22.13)

Производная dx/dt = u это скорость перемещения точки огибающей, фаза которой постоянна, т.е. групповая скорость. Так как w = v∙k, то 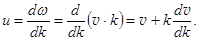(22.14)

Но k = 2pçl, dk = (–2pçl²)dl. Отсюда 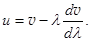Формула Рэлея, 1881 (22.15)

Эту формулу Рэлей получил в 1881 году. Производная dvçdl определяет дисперсию среды. Суть ее в том, что монохроматические волны разных длин распространяются в диспергирующей среде с разными скоростями v.

Рассмотрим соотношение между фазовой и групповой скоростями в средах с разной дисперсией.

5. Среда с нормальной дисперсией. Показатель преломления n в такой среде с увеличением длины волны l уменьшается, то есть dnçdl < 0. Так как n = сçv, то это соответствует dvçdl > 0. С увеличением длины волны l фазовая скорость монохроматических волн в среде с нормальной дисперсией увеличивается. По мере движения в такой среде группа волн расплывается. Длинноволновые элементарные цуги уходят вперед, а коротковолновые отстают. В результате групповой цуг становится длиннее. Как видно из формулы Рэлея, групповая скорость в этом случае меньше фазовой. Это значит, что при движении цуга в его хвостовой части возникают все новые максимумы, которые постепенно перемещаются вперед, достигают его головной части и там исчезают. В системе отсчета, связанным с групповым цугом, гребни в цуге бегут вперед.

При всех методах измерения скорости света измеряется групповая скорость светового импульса или, как часто говорят, скорость сигнала. При преломлении света на границе раздела сред играет роль фазовая скорость. Монохроматические волны разных длин преломляются по-разному.

Если измерить фазовую скорость света v в какой-либо среде по преломлению света (говорят, рефрактометрическим путем) и измерить скорость распространения светового сигнала u в этой среде каким-либо лабораторным методом, то можно проверить формулу Рэлея. Впервые это сделал Майкельсон для сероуглерода. Формула подтвердилась с точностью до двух знаков.

Качественно опережение длинноволновых элементарных цугов в группе светового импульса наблюдали в 1881 году Юнг и Форбс. Они измеряли скорость света методом Физо. При измерениях в белом свете они обнаружили окрашивание зубца при появлении света в красный свет, а при исчезновении в голубой.

Если в среде с нормальной дисперсией перемещается группа циркулярно поляризованных в одном направлении волн, то расплывание волнового пакета поводит к тому, что “пружина” годографа 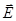как бы раскручивается. Витки относительно пружины перемещаются вперед, а шаг между витками в передней части цуга увеличивается. Увеличивается и длина “пружины”.

6. Среда с аномальной дисперсией. В этом случае dnçdl > 0, dvçdl < 0, Групповая скорость больше фазовой. Гребни в цуге светового импульса перемещаются из головной части в хвостовую.

Случай аномальной дисперсии представляет, в основном, чисто теоретический интерес. Дело в том, что аномальная дисперсия находится в области резонансного поглощения. При этом деформация светового импульса происходит так быстро, что понятие групповой скорости теряет физический смысл.

7. Дисперсия межзвездной среды. Дисперсию космической среды пытался установить еще Араго. С этой целью он наблюдал переменную звезду Алголь (b Персея, период изменения блеска 2,867 суток). Если бы межзвездная среда (по представлению Араго - вакуум) обладала дисперсией, то на таком огромном расстоянии (36 парсеков или 117.4 световых лет) эффект расползания волнового пакета был бы замечен невооруженным глазом. При нарастании яркости звезда должна была показаться красной, при убывании – голубой.

Однако до сих пор при наблюдении обычных переменных звезд таких эффектов не обнаружено. Поэтому полагается, что дисперсии света в вакууме нет. Групповая и фазовая скорости в вакууме одинаковы.

В 1967 году были открыты пульсары – пульсирующие источники радиоизлучения, периоды которых составляют от долей до нескольких секунд. Почти сразу же было обнаружено, что длинноволновые сигналы в сантиметровом диапазоне доходят от пульсаров до земли медленнее коротковолновых. Это объясняется влиянием межзвездной плазмы, через которую проходит сигнал.

Межзвездная плазма – чрезвычайно разреженный газ, состоящий из электрически заряженных частиц, в основном, электронов. По отношению к электромагнитным волнам плазма ведет себя как среда, показатель преломления которой меньше единицы, n < 1 (на рис.183 это состояние соответствует правой ветви NP). Фазовая скорость волны в плазме v = сçn всегда больше скорости света в вакууме.

Поскольку частицы плазмы свободны и не входят в состав атомов, характер их колебаний под действием поля волны отличен от колебаний электронов в атоме. Поэтому зависимость между групповой и фазовой скоростями выглядит иначе: u = с²çv. (22.16)

Дисперсия плазмы нормальная, фазовая скорость волны в плазме с увеличением l растет. Поэтому скорость группы волн по мере увеличения их средней волны l уменьшается.

Запаздывание длинноволновых сигналов от коротковолновых объясняется меньшей скоростью длинноволновых пакетов по сравнению с коротковолновыми пакетами.