ГЛАВА 7. РАССЕЯНИЕ СВЕТА И ОПТИЧЕСКИЕ ЯВЛЕНИЯ В АТМОСФЕРЕ

Рассеяние света

1. Оптические неоднородности среды. Среда является оптически однородной, если любой элемент её объёма имеет постоянное для данной среды значение показателя преломления n. Это значит, что поляризуемость среды в любой точке есть величина постоянная.

Когда ЭМ волна распространяется в оптически однородной среде, то одинаковые дифференциальные объёмы среды, находящиеся на фронте волны, испускают когерентные вторичные волны одинаковой интенсивности. Интерференция этих волн в боковых направлениях происходит в соответствии с теорией Френеля и приводит к полному гашению света. Поэтому в идеальной оптически однородной среде не должно быть рассеяния света.

В модели квазиупругих резонаторов физическими центрами френелевских вторичных когерентных волн являются оптические электроны. Поэтому идеальной оптически однородной среде соответствует система одинаковых резонаторов, равномерно распределённых в пространстве.

В оптически неоднородной среде имеются разные резонаторы, поэтому вторичные волны, испускаемые оптическими электронами в разных точках волнового фронта, имеют разную интенсивность. Интерференция вторичных волн не приводит в этом случае к полному гашению света. В результате возникает рассеянный свет.

2. Мутные среды – это среды, оптически неоднородные и интенсивно рассеивающие свет. По физико-химическим свойства мутные среды делятся на аэрозоли – дымы (твёрдые частицы в газе) и туманы (жидкие частицы в газе), гидрозоли – взвеси (мелкие твёрдые частицы в жидкости) и эмульсии (жидкие частицы в жидкости), твёрдые тела – опалы, перламутры, молочные стёкла.

3. Опытные законы рассеяния света. Впервые рассеяние света в мутных средах изучал в 1869 году Джон Тиндаль. По данным его и других исследователей опытов, которые были выполнены с мутными средами, содержащими рассеивающие частицы размером не более 0,2λ в малой концентрации, можно сформулировать следующие опытные законы.

а. Чем короче длина волны λ, тем интенсивнее рассеивается свет. Если рассеяние наблюдается в белом свете, то рассеянный свет имеет сине-голубой оттенок.

б. Свет, рассеянный под прямым углом к первичному пучку естественного света, полностью или почти полностью линейно поляризован.

в. Кривая интенсивности рассеянного света (индикатриса рассеяния) симметрична относительно направлений первичного пучка и перпендикулярному ему (рис.195).

Здесь ОХ - направление первичного пучка, ОN - направление, перпендикулярное к направлению первичного пучка.

Направления OX и ОN являются осями симметрии индикатрисы.

4. Теория рассеяния Рэлея. Первый вариант теории ещё в упругой модели света Рэлей разработал в 1891 г. Позднее он переработал её применительно к ЭМ модели света. Основные результаты совпали в обеих теориях.

В электромагнитной теории рассеяния, которая была построена к 1899 году, Рэлей рассматривал распространение световой электромагнитной волны в сплошной прозрачной среде, диэлектрическая проницаемость которой ε. В этой среде равномерно вкраплены рассеивающие частицы – диэлектрические шарики радиусом R, проницаемость которых ε₁ отлична от проницаемости среды ε.

Рэлей полагал, что размер шариков много меньше длины волны света, R << λ, а расстояния между шариками достаточно велики для того, чтобы можно было пренебречь взаимодействием между ними.

Проходящий свет дифрагирует на шариках, при этом вторичные волны, исходящие от разных рассеивающих свет частиц, взаимно когерентны. Поэтому интенсивность I_j рассеянного света Рэлей вычислял суммированием амплитуд рассеянных волн.

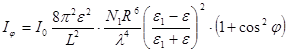. Формула Рэлея, 1899(24.1)

Здесь I₀ - интенсивность падающего света, L - расстояние от рассеивающего объекта до точки наблюдения, N₁ - концентрация рассеивающих шариков, λ - длина волны света.

Из формулы Рэлея следуют два важных вывода.

а. Интенсивность рассеянного света пропорциональна шестой степени радиуса рассеивающих частиц. С увеличением размера частиц рассеяние быстро увеличивается.

б. Чем короче световые волны, тем сильнее они рассеиваются. Зависимость

I_расс~1çl⁴ называют законом Рэлея. (24.2)

5. Молекулярное рассеяние света. Дальнейшие исследования показали, что наличие мелких частиц пыли и тумана не является единственной причиной рассеяния света. Из наблюдений в горных обсерваториях следовало, что голубизна неба не уменьшается с уменьшением загрязнённости воздуха. Наоборот, чем чище воздух, тем интенсивнее рассеянный свет. Выяснилось, что рассеяние света происходит и в физически однородных средах - чистых газах, чистых жидкостях, чистых кристаллах.

В 1908 г. Мариан Смолуховский показал, что оптическими неоднородностями могут быть не только какие-то инородные вкрапления, но и флуктуации плотности среды, то есть случайные колебания плотности в малых объёмах около её среднего значения. Рассеяние на флуктуациях плотности среды стали называть молекулярным рассеянием.

В 1910 г. Альберт Эйнштейн, исходя из идеи Смолуховского, разработал теорию флуктуационного рассеяния в жидкостях. В качестве центров вторичных волн он принимал не отдельные молекулы, а их коллективы в объёмах, размеры которых много меньше длины волны. Для интенсивности рассеянного света в жидкостях Эйнштейна получил формулу: 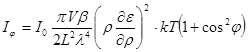. Формула Эйнштейна для жидкостей, 1910 (24.3)

Здесь V - рассеивающий объём, β - изотермический коэффициент сжимаемости среды, ρ - её плотность, ε - диэлектрическая проницаемость, k – пост. Больцмана, T - температура.

Из формулы (24.3) молекулярного рассеяния в жидкостях можно получить и формулу молекулярного рассеяния света в газах. Показатель преломления газов очень мало отличается от единицы. Например, воздух при нормальных условиях имеет n = 1,000292. Так же мало отличается от единицы и диэлектрическая проницаемость ε = n². Для воздуха, например, ε = n² = 1,000584, плотность ρ = 1,293 кг/м³.Если в формуле удельной рефракции (21.11) вместо n² поставить ε и пренебречь десятичными знаками в знаменателе, то получаем: ε – 1 = сonst = a = 4,52·10^–4 м³/кг. Продифференцировав ε = 1 + aρ по плотности ρ, 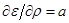, и подставив в формулу (24.3), получаем интенсивность молекулярного рассеяния света в газах. 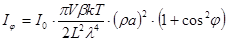. Формула Эйнштейна для газов (24.4)

При молекулярном рассеянии так же выполняется закон Рэлея I_расс~1çλ⁴.

Наиболее интенсивное рассеяние света на флуктуациях плотности наблюдается в средах при критических температурах. Это явление сильного рассеяния света называют критической опалесценцией. Смолуховский объяснил его тем, что сжимаемость вещества в критической точке очень велика. Поэтому в веществе легко возникают значительные флуктуации плотности в малых объёмах. Вещество в критическом состоянии приобретает ярко выраженную оптическую неоднородность.

Теория рэлеевского и молекулярного рассеяния объясняет два из трёх опытных законов. Во-первых, законом Рэлея I ~ 1çλ⁴ объясняется голубоватый цвет рассеянного белого света, а во-вторых, математически строго вытекает индикатриса рассеяния 1 + сos²φ.

Факт поляризации рассеянного света требует особого рассмотрения.

6. Рассеяние на изотропных молекулах. Рассмотрим молекулярное рассеяние в среде, состоящей из изотропных молекул. Изотропными здесь являются молекулы, поляризуемость которых во всех направлениях одинакова. В этом случае любой дифференциальный объём рассеивающей среды является оптически однородным. Понятие “дифференциальный объём” означает такой объём среды, в котором содержится достаточно много молекул, чтобы можно было считать этот объём однородным объёмом жидкости или газа, но не группой отдельных молекул. В то же время этот объём много меньше объёма λ³, так, чтобы линейная протяжённость сферического объёма не превышала 0,1λ.

Рассмотрим рассеяние поляризованного и неполяризованного света.

а. Рассеяние линейно поляризованного света. Пусть на изотропную молекулу О падает плоская линейно поляризованная в плоскости XOY электромагнитная волна. Под действием переменного поля этой волны оптический электрон молекулы колеблется вдоль оси OY с той же частотой, что и волна.

В свою очередь, электрон излучает электромагнитное поле в тех направлениях, по отношению к которым поперечная составляющая колебаний электрона не равна нулю. То есть электрон не излучает лишь в направлении оси OY, вдоль которой он колеблется.

Амплитуда излучаемой в каком-либо направлении волны определяется проекцией амплитуды колебаний электрона на плоскость, перпендикулярную к данному направлению (рис.196). Чем ближе к оси OY это направление, тем меньше интенсивность рассеиваемой волны. Максимальную интенсивность имеет рассеянная волна в направлении оси OZ.

В результате рассеяния энергия падающей волны уменьшается. Если падающая волна линейно поляризована, то в случае изотропных молекул рассеянные волны так же линейно поляризованы.

б. Рассеяние естественного света. Пусть на изотропную молекулу O падает плоская неполяризованная электромагнитная волна естественного света. В естественном свете векторы 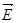разных волн колеблются по диаметрам круга (рис.197). Лишь в плоскости ZOY круг, в пределах которого колеблются электроны, проектируется в прямую линию. Поэтому свет, рассеянный в плоскости ZOY, полностью поляризован.

Во всех других направлениях круг проектируется в эллипс. Степень поляризации света в этих направлениях не равна единице. Она зависит от величины полуосей эллипса. Чем ближе угол φ к 90°, тем больше степень поляризации света.

7. Рассеяние света на анизотропных молекулах. Предположим, что молекула имеет единственное направление, вдоль которого она может поляризоваться. Такой случай полной анизотропии молекулы называют моделью жёсткой палочки. Поляризуемость такой молекулы во всех направлениях, кроме одного, равна нулю.

а. Рассеяние на анизотропных молекулах линейно поляризованного света. Пусть на анизотропную молекулу AB, лежащую в плоскости XOY под углом θ к оси OY, падает волна, вектор Е которой колеблется так же в плоскости XOY (рис.198). Вынужденные колебания молекулы совершаются вдоль направления AB под действием проекции вектора Е на ось диполя, E₁ = E сosθ.

Колебания молекулярного диполя возбуждают, в свою очередь, в направлении OZ две линейно поляризованные волны. У одной вектор Е колеблется вдоль оси OY, у другой - вдоль оси OX. Рассеянный анизотропной молекулой свет в направлении оси OZ, отличается от света, рассеянного изотропной молекулой. В случае изотропной молекулы вектор Е рассеянного вдоль оси OZ света колеблется исключительно в плоскости YOZ независимо от того, поляризованный или неполяризованный свет рассеивается.

В случае анизотропной молекулы в рассеянном в направлении оси OZ свете наряду с компонентой E_y появляется компонента E_x, зависящая от угла θ. Происходит деполяризация света. Количественно деполяризация определяется величиной Δ = I_xçI_y , называемой коэффициентом деполяризации. Здесь I_x и I_y - интенсивности рассеянного света вдоль оси OZ, вектор Е которого колеблется параллельно оси OХ и оси OY.

б. Рассеяние на анизотропных молекулах естественного света усложняется за счёт появления в падающем свете компоненты Е вдоль оси OZ. Но деполяризация света, рассеянного вдоль оси OZ, так же имеет место, хотя и несколько отличается от деполяризации при рассеянии линейно поляризованного света.

Если среда состоит из анизотропных молекул, то из-за теплового движения помимо флуктуаций плотности возникают также флуктуации анизотропии. Свет, рассеянный на флуктуациях анизотропии, деполяризован. При рассеянии линейно поляризованного света на флуктуациях анизотропии коэффициент деполяризации Δ = 0,75, а при рассеянии естественного света Δ = 0,86 в направлении оси OZ.

Суммарная деполяризация при рассеянии на флуктуациях плотности и флуктуациях анизотропии меньше. У водорода H₂ Δ = 0,01, у азота N₂ Δ = 0,04, у газа CO₂ Δ = 0,07. В жидкостях степень деполяризации больше. В бензоле C₆H₆ Δ = 0,44, в сероуглероде CS₂ Δ = 0,68, в нитротолуоле C₆H₅CH₂NO₂ Δ = 0,80.

8. Теория рассеяния Ми. Строгую теорию рассеяния света круглыми диэлектрическими частицами, размер которых может достигать величины одного порядка с длиной волны λ, построил в 1908 году Густав Ми на основе дифракции света. Теория Ми включает рэлеевское рассеяние, подчиняющиеся закону I_расс~1çλ⁴, как частный случай, когда размер шариков много меньше длины волны света, R << λ.

С увеличением радиуса шариков R до R ~ λ и более при ε₁>1 (шариков) теория Ми обнаружила резкие максимумы и минимумы рассеяния (резонансы Ми), когда 2R = kλ, где k = 1,2,3... Симметричность индикатрисы рассеяния в этом случае нарушается, рассеяние вперёд усиливается, назад - ослабевает. Зависимость поляризации света от угла рассеяния сильно усложняется. Рассеяние света большими частицами, когда R >> λ, в значительной степени обусловлено законами геометрической оптики с учётом интерференции лучей, отражённых и преломлённых на поверхности частиц. Этот вид рассеяния обуславливает такие оптические явления, как ореолы, радуги, гало.

Итак, теория Ми выделяет 3 основных области рассеяния. При R < 0,01λ преобладает рэлеевское рассеяние, при R в интервале от 0,01λ до λ преобладает дифракционное рассеяние и при R > λ - геометрическое рассеяние.

9. Экстинкция. В результате рассеяния света в стороны интенсивность светового пучка убывает быстрее, чем при наличии одного поглощения. Поэтому в формуле закона Бугера (22.3) наряду с коэффициентом истинного поглощения χ должен стоять добавочный коэффициент χ', обусловленный рассеянием. 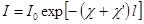. (24.5)

Величину χ' называют коэффициентом рассеяния. Сумму коэффициентов поглощения χ и рассеяния χ' называют коэффициентом экстинкции (от лат. exstinctio - гашение). Само явление ослабления пучка света при его распространении в веществе за счёт совместного действия поглощения и рассеяния называют экстинкцией.

10. Рассеяние света - исключительно разнообразный по механизму и формам проявления оптический эффект. Процесс рассеяния света тесно связан со строением вещества. Поэтому последовательная теория рассеяния света может быть разработана только с учётом квантовых свойств света и структуры рассеивающей материи.