Волновая оптика. Интерференция света
В лекции №3, при рассмотрении сложения одинаково направленных колебаний с частотами 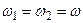 , отмечалось, что результирующие колебания являются также гармоническими с той же w и амплитудой А, зависящей от разности фаз
, отмечалось, что результирующие колебания являются также гармоническими с той же w и амплитудой А, зависящей от разности фаз 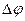 исходных колебаний (
исходных колебаний ( 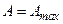 при
при 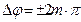 и
и 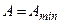 при
при 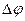 =
= 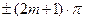 , где m - целое число).
, где m - целое число).
Интерференция - явление сложения волн одинаковой природы, при котором в области их пересечения наблюдается устойчивое распределение амплитуды результирующих колебаний, т.е. происходит пространственное перераспределение энергии волн. Поскольку свет является волновым процессом, то явление интерференции свойственно и для него. Однако наблюдать интерференцию света можно лишь при выполнении определённых условий. Каких же? Во-первых, интерферирующие световые волны должны быть монохроматическими, т.е. должны иметь бесконечно узкие частотные спектры 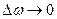 , при соблюдении равенства
, при соблюдении равенства 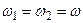 ; во-вторых, эти волны должны быть когерентными, т.е. разность их фаз
; во-вторых, эти волны должны быть когерентными, т.е. разность их фаз 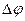 в любой точке области пересечения не должна изменяться со временем; в-третьих, волны должны иметь одинаковую поляризацию, т.е. иметь ненулевые соответствующие компоненты векторов
в любой точке области пересечения не должна изменяться со временем; в-третьих, волны должны иметь одинаковую поляризацию, т.е. иметь ненулевые соответствующие компоненты векторов 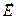 и
и 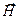 ).
).
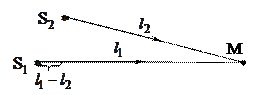 Рассмотрим процесс сложения двух когерентных волн, характеризуемых амплитудами А1, А2и частотами
Рассмотрим процесс сложения двух когерентных волн, характеризуемых амплитудами А1, А2и частотами 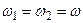 . Пусть два пространственно разнесённых источника волн находятся в некоторой упругой среде (не случайно Гюйгенс придумал эфир!). Тогда, в произвольной точке М области пересечения волн, частицы среды участвуют одновременно в двух колебательных процессах (вдоль оси y):
. Пусть два пространственно разнесённых источника волн находятся в некоторой упругой среде (не случайно Гюйгенс придумал эфир!). Тогда, в произвольной точке М области пересечения волн, частицы среды участвуют одновременно в двух колебательных процессах (вдоль оси y):
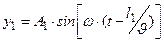 и
и 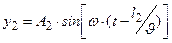 ,
,
где J - скорость волны в среде.
Учитывая, что 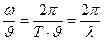 , можно записать:
, можно записать:
|
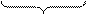
|
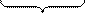
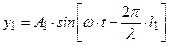 и
и 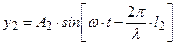 .
.
В лекции №3 показано, что результат сложения таких колебаний есть также гармонические колебания:
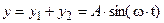 ,
,
где 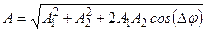 ;
; 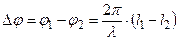 . При
. При 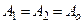 получим
получим 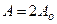 , если
, если 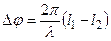 = 2mp , т.е. если
= 2mp , т.е. если  ; и A=0, если
; и A=0, если 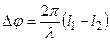 = (2m+1)×p, т.е. если
= (2m+1)×p, т.е. если 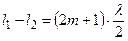 .
.
Величину 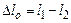 называют геометрической разностью хода интерферирующих лучей. Если же лучи распространяются в среде с показателем преломления
называют геометрической разностью хода интерферирующих лучей. Если же лучи распространяются в среде с показателем преломления 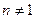 , тогеометрическую разность хода, следует заменить на оптическую разность хода
, тогеометрическую разность хода, следует заменить на оптическую разность хода 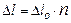 . Тогда, условия максимума и минимума амплитуды результирующих колебаний при интерференции принимают вид:
. Тогда, условия максимума и минимума амплитуды результирующих колебаний при интерференции принимают вид: 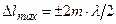 для максимума и
для максимума и 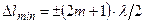 для минимума.
для минимума.
Обычно источником света являются нагретые тела, точнее релаксирующие (переходящие с верхних в нижние энергетические состояния) атомы и молекулы этих тел. Согласовать процессы релаксации огромного числа частиц невозможно, поэтому нагретые тела испускают некогерентные и немонохроматические световые волны. До появления лазеров (в которых всё-таки удаётся согласовать процессы релаксации большого числа атомов) для наблюдения интерференции света когерентные пучки получали разделением волн и последующим сведением лучей, исходящих от одного и того же источника. Рассмотрим некоторые из этих методов.
а)Метод Юнга(английский врач, 1802 г.). Непрозрачный экран с двумя щелями, равноудалёнными от оси на расстояние 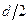 , освещают монохроматической плоской световой волной, исходящей от удалённого источника.
, освещают монохроматической плоской световой волной, исходящей от удалённого источника.
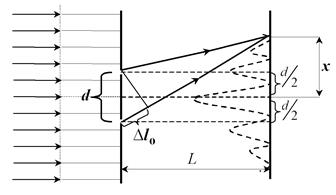
Щели, будучи расположенными на одном волновом фронте, сами являются источниками когерентных световых волн (согласно принципу Гюйгенса-Френеля). В результате интерференции волн, исходящих от щелей, на втором экране, расположенном параллельно первому на расстоянии L, можно наблюдать чередующиеся тёмные и светлые полосы (совокупность этих полос называют интерференционной картиной). Рассчитаем удаление полос от оси в случае, если окружающая среда - воздух: 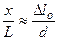
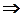
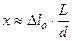 . Откуда, учитывая выше полученные соотношения для
. Откуда, учитывая выше полученные соотношения для 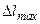 и
и 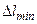 , получим:
, получим: 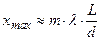 и
и 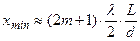 .
.
Если свет немонохроматический, то интерференционная картина - набор чередующихся окрашенных полос, т.к. значения 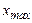 и
и 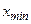 зависят от длины волны l.
зависят от длины волны l.
 б)Метод Френеля (1816 г.). Свет от источника S падает расходящимся пучком на два плоских зеркала, распложенных относительно друг друга под углом, немного меньшим 180о. Отражённые лучи когерентны и поэтому могут интерферировать. Интерференционную картину наблюдают на экране, расстояние от которого до разных точек зеркал, различно, что и обусловливает постепенное изменение оптической разности хода Dl между интерферирующими лучами.
б)Метод Френеля (1816 г.). Свет от источника S падает расходящимся пучком на два плоских зеркала, распложенных относительно друг друга под углом, немного меньшим 180о. Отражённые лучи когерентны и поэтому могут интерферировать. Интерференционную картину наблюдают на экране, расстояние от которого до разных точек зеркал, различно, что и обусловливает постепенное изменение оптической разности хода Dl между интерферирующими лучами.
в)Интерференция света в тонких плёнках(метод Ньютона). Часто можно наблюдать радужную окраску масляных плёнок на воде, мыльных пузырей, крылышек насекомых и т.п., возникающие в результате интерференции света, отражённого поверхностями плёнки. Падающий пучок, отражаясь от обеих поверх-ностей плёнки, расщепляется на два когерентных пучка (1 и 2), которые и интерферируют в отражённом свете. Оптическая разность хода Dl, возникающая между интерферирующими лучами, равна:
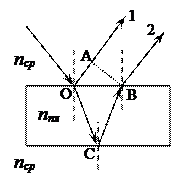 Dl =
Dl = 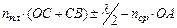 , где слагаемое
, где слагаемое 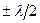 обусловлено потерей полуволны при отражении света от границы раздела с оптически более плотной средой: при
обусловлено потерей полуволны при отражении света от границы раздела с оптически более плотной средой: при 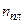 >
> 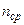 надо взять (-), при nпл< ncр ¾ (+).
надо взять (-), при nпл< ncр ¾ (+).
при иьные ответствующие компоненты ациютов по тов 12.1.2. Применения интерференции света
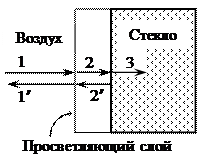 1) Просветление линз. При прохождении через каждую поверхность линзы свет теряет в результате отражения
1) Просветление линз. При прохождении через каждую поверхность линзы свет теряет в результате отражения 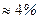 своей интенсивности, т.е. »10% на каждой линзе. Если линз в приборе много, то это приводит к недопустимому снижению светосилы прибора. Кроме того, отражения от линз приводят к нежелательным бликам. Устраняют эти недостатки "просветлением" линз. Для этого на их поверхности наносят плёнки с показателем преломления
своей интенсивности, т.е. »10% на каждой линзе. Если линз в приборе много, то это приводит к недопустимому снижению светосилы прибора. Кроме того, отражения от линз приводят к нежелательным бликам. Устраняют эти недостатки "просветлением" линз. Для этого на их поверхности наносят плёнки с показателем преломления 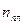 , меньшим, чем у материала линзы. При отражении света от границ раздела "воздух – плёнка" и "плёнка - стекло" возникает интерференция когерентных лучей 1'и2'. Толщину плёнки d и соотношение показателей преломления стекла
, меньшим, чем у материала линзы. При отражении света от границ раздела "воздух – плёнка" и "плёнка - стекло" возникает интерференция когерентных лучей 1'и2'. Толщину плёнки d и соотношение показателей преломления стекла 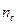 и плёнки
и плёнки 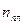 можно подобрать так, чтобы волны, отражённые от обеих поверхностей плёнки, гасили друг друга. Для этого их амплитуды должны быть равны (что выполняется при
можно подобрать так, чтобы волны, отражённые от обеих поверхностей плёнки, гасили друг друга. Для этого их амплитуды должны быть равны (что выполняется при 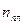 =
= 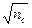 ), а оптическая разность хода
), а оптическая разность хода 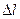 =
= 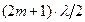 . Так как
. Так как 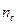 >
> 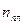 >
> 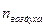 , то потеря
, то потеря 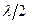 происходит на обеих поверхностях; следовательно, условие минимума (при нормальном падении света) имеет вид:
происходит на обеих поверхностях; следовательно, условие минимума (при нормальном падении света) имеет вид: 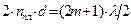 . Обычно принимают
. Обычно принимают 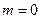 , тогда просветляющая плёнка должна удовлетворять требованию
, тогда просветляющая плёнка должна удовлетворять требованию 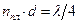 . Так как добиться одновременного гашения для всех l невозможно, то просветляющее покрытие оптимизируют для l=0,55мкм (зелёный цвет), к которой глаз наиболее чувствителен. Для света же с другими l условие гашения выполняется не точно, поэтому просветлённые объективы в отражённом свете имеют синевато-красный оттенок.
. Так как добиться одновременного гашения для всех l невозможно, то просветляющее покрытие оптимизируют для l=0,55мкм (зелёный цвет), к которой глаз наиболее чувствителен. Для света же с другими l условие гашения выполняется не точно, поэтому просветлённые объективы в отражённом свете имеют синевато-красный оттенок.
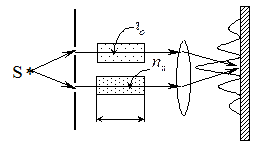 2) Интерферометрия- оптический метод точного определения расстояния (точность
2) Интерферометрия- оптический метод точного определения расстояния (точность 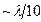 ) и показателя преломления (точность
) и показателя преломления (точность 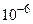 ). Для этого используют приборы - интерферометры. На пути интерферирующих лучей располагают две одинаковые кюветы длиной l, одна из которых заполнена газом с известным показателем преломления
). Для этого используют приборы - интерферометры. На пути интерферирующих лучей располагают две одинаковые кюветы длиной l, одна из которых заполнена газом с известным показателем преломления 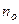 , а другая - исследуемым газом с неизвестным
, а другая - исследуемым газом с неизвестным 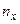 . Между лучами возникает оптическая разность хода Dl =
. Между лучами возникает оптическая разность хода Dl = 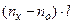 , что приводит к сдвигу интерференционных полос на экране (по сравнению с положением этих полос до установки кювет). По величине сдвига рассчитывают
, что приводит к сдвигу интерференционных полос на экране (по сравнению с положением этих полос до установки кювет). По величине сдвига рассчитывают 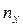 .
.
Кроме перечисленного, интерферометры применяются для контроля качества поверхностей, измерения углов, смещений, для исследования быстропротекающих процессов. Применяя интерферометр, Майкельсон доказал, что "эфира" нет. С помощью интерферометров исследовали распространение света в движущихся телах, что позволило экспериментально подтвердить справедливость теории относительности.
12.2. Дифракция света
 Дифракцией называют явление перераспределения энергии в отражённом и прошедшем излучении, возникающее вследствие интерференции вторичных (относительно падающей волны) волн. В упрощённой интерпретации, явлением дифракции называют огибание волнами препятствий. Действительно, вследствие дифракции волны могут попадать в область геометрической тени (огибать препятствия), проникать через небольшие отверстия в экранах и т.д. Например, звук хорошо слышен за углом дома, т.е. звуковая волна его огибает. Явление дифракции характерно и для света, как объекта, имеющего волновую природу. Например, светлое пятно, полученное при освещении экрана через отверстие, не имеет резкой тени. Это особенно заметно при
Дифракцией называют явление перераспределения энергии в отражённом и прошедшем излучении, возникающее вследствие интерференции вторичных (относительно падающей волны) волн. В упрощённой интерпретации, явлением дифракции называют огибание волнами препятствий. Действительно, вследствие дифракции волны могут попадать в область геометрической тени (огибать препятствия), проникать через небольшие отверстия в экранах и т.д. Например, звук хорошо слышен за углом дома, т.е. звуковая волна его огибает. Явление дифракции характерно и для света, как объекта, имеющего волновую природу. Например, светлое пятно, полученное при освещении экрана через отверстие, не имеет резкой тени. Это особенно заметно при 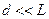 (где
(где 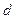 -размер отверстия), когда светлое пятно на экране представляется состоящим из чередующихся светлых и тёмных колец. При использовании белого света дифракционная картина приобретает радужную окраску. Отметим, что сравнимость размера преграды с длиной волны света l не является необходимым условием для наблюдения дифракции.
-размер отверстия), когда светлое пятно на экране представляется состоящим из чередующихся светлых и тёмных колец. При использовании белого света дифракционная картина приобретает радужную окраску. Отметим, что сравнимость размера преграды с длиной волны света l не является необходимым условием для наблюдения дифракции.
Дифракционные картины можно наблюдать и в естественных условиях, например: 1) цветные кольца, окружающие источник света, наблюдаемый сквозь туман или запотевшее стекло, обусловлены дифракцией света на мелких каплях воды; 2) радужный ореол Солнца в морозный день - из-за дифракции света на мелких кристалликах льда; 3) радужные ореолы светящихся предметов при глазных заболеваниях - из-за помутнения прозрачного тела глаза и дифракции света на образовавшихся в этом теле мелких неоднородностях.
Метод зон Френеля.Рассмотрим процесс дифракции света на щели (входном отверстии или диафрагме оптического прибора) более детально. Пусть плоская монохроматическая волна падает на щель размеромd (см. рис. ниже). Согласно принципу Гюйгенса-Френеля, каждая точка волнового фронта на входном отверстии является источником вторичных сферических волн, лучи которых расходятся за экраном по всем направлениям. Для любой пары симметричных лучей, падающих на экран в точке О оптическая разность хода Dl равна нулю, поэтому в этой точке освещённость увеличивается – светлая полоса с интенсивностью Io.
Выберем такое направление j1, при котором лучи фокусируются линзой в точку О1, а разность хода между крайними лучами отверстия 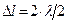 . Тогда, весь пучок можно разделить на две равные зоны IиII, называемые зонами Френеля, и представляющими собой участок волнового фронта, для которого разность фаз между крайними лучами, поступающими в точку наблюдения, равна p, что соответствует разности хода лучей Dl=
. Тогда, весь пучок можно разделить на две равные зоны IиII, называемые зонами Френеля, и представляющими собой участок волнового фронта, для которого разность фаз между крайними лучами, поступающими в точку наблюдения, равна p, что соответствует разности хода лучей Dl= 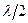 . Поэтому вторичные волны, излучаемые соответствующими точками соседних зон, колеблются в точке O1 в противофазе и гасят друг друга. В результате в точке О1 – нулевая освещённость.
. Поэтому вторичные волны, излучаемые соответствующими точками соседних зон, колеблются в точке O1 в противофазе и гасят друг друга. В результате в точке О1 – нулевая освещённость.
Рассмотрим теперь пучок, дифрагирующий под углом j2, для которого разность хода Dl между крайними лучами равна 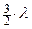 . Тогда весь волновой фронт этого пучка можно разделить на три зоны Френеля. Соответствующие лучи от двух соседних зон, имеющие оптическую разность хода равную
. Тогда весь волновой фронт этого пучка можно разделить на три зоны Френеля. Соответствующие лучи от двух соседних зон, имеющие оптическую разность хода равную 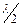 , взаимно попарно погасятся, и поэтому точка O2окажется освещена только лучами III зоны. Причём, интенсивность света в точке O2 составляет только 1/3 от интенсивности света в точке O.
, взаимно попарно погасятся, и поэтому точка O2окажется освещена только лучами III зоны. Причём, интенсивность света в точке O2 составляет только 1/3 от интенсивности света в точке O.
 Лучи, приходящие в точку O3 экрана, дифрагируют из щели под углом j3, причём разность хода между крайними лучами в таком пучке составляет 2l. Поэтому весь волновой фронт пучка можно разбить на 4 зоны Френеля. Соответствующие лучи зон I и II, III и IV, имея оптическую разность хода, равную
Лучи, приходящие в точку O3 экрана, дифрагируют из щели под углом j3, причём разность хода между крайними лучами в таком пучке составляет 2l. Поэтому весь волновой фронт пучка можно разбить на 4 зоны Френеля. Соответствующие лучи зон I и II, III и IV, имея оптическую разность хода, равную 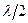 , взаимно попарно погасятся, и в точке О3 получим нулевую освещённость.
, взаимно попарно погасятся, и в точке О3 получим нулевую освещённость.
Для пучка, дифрагирующего под углом 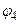 , оптическая разность хода между крайними лучами составит
, оптическая разность хода между крайними лучами составит 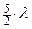 , соответственно весь световой пучок можно разбить на 5 зон Френеля. Лучи от первых четырёх зон взаимно погасятся и точка О4будет освещена только лучами Vзоны с интенсивностью
, соответственно весь световой пучок можно разбить на 5 зон Френеля. Лучи от первых четырёх зон взаимно погасятся и точка О4будет освещена только лучами Vзоны с интенсивностью 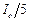 .
.
Экстраполируя аналогичные рассуждения на другие направления дифракции, можно утверждать, что пучки лучей, дифрагирующих под углами, соответствующими нечётному числу зон Френеля, создают на экране дифракционные максимумы, а пучки лучей, дифрагирующих под углами, соответствующими чётному числу зон Френеля, создают дифракционные минимумы. Причём, освещённость максимумов уменьшается при увеличении угла дифракции лучей.
Получим формулы для расчёта углов j, соответствующих светлым и тёмным полосам на экране (окружающая среда - воздух): светлым полосам соответствует 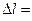
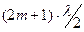 , а тёмным
, а тёмным 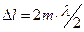 . Учитывая, что для воздуха n=1 и
. Учитывая, что для воздуха n=1 и 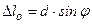 , окончательно получим, что светлым полосам соответствуют такие направления, для которых
, окончательно получим, что светлым полосам соответствуют такие направления, для которых 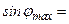
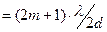 , а тёмным -
, а тёмным - 
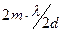 , где m - порядок дифракционного максимума или минимума (целое число).
, где m - порядок дифракционного максимума или минимума (целое число).
При дифракции плоской электромагнитной волны на множестве параллельных щелей (дифракционной решётке) дифракционные максимумы (светлые полосы) получаются более яркими и узкими, а разделяющие их минимумы (тёмные полосы) - более широкими и тёмными.
Положение главных максимумов зависит от длины волны l. Поэтому, при пропускании через решётку белого света, все максимумы, кроме центрального с 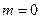 , разложатся в спектр, фиолетовая область которого обращена к центру дифракционной картины, а красная - наружу. Это свойство дифракционной решётки используют для исследования спектрального состава света.
, разложатся в спектр, фиолетовая область которого обращена к центру дифракционной картины, а красная - наружу. Это свойство дифракционной решётки используют для исследования спектрального состава света.
Дата добавления: 2019-12-09; просмотров: 832;