Понятия корреляции и регрессии

В промышленном производстве приходится иметь дело со многими явлениями, имеющими вероятностный характер. Например, к числу случайных величин можно отнести: стоимость продукции, доходы предприятия, межремонтный пробег автомобилей, время ремонта оборудования и т. д. Большинство явлений и процессов в машиностроении находятся в постоянной взаимной и всеохватывающей связи. Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль. Оно дает возможность глубже понять сложный механизм причинно-следственных отношений между явления.

Выявление зависимостей показателей эффективности работы от различных управляемых факторов связано с обработкой огромных объемов статистической информации. Выделение в этой массе информации причинных связей между различными показателями представляет существенную ценность. Для решения этой задачи целесообразно использовать методы регрессионного анализа.

Регрессионным анализомназывают систему методов оценки (расчета) параметров регрессии – коэффициентов регрессии на основе имеющихся наблюдений. Регрессией называется односторонняя вероятностная зависимость между случайными величинами, которая выражается с помощью некоторой функции.

Различают два вида зависимости между показателями: функциональную и корреляционную.

Функциональная зависимостьпроявляется определенно и точно в каждом конкретном случае, в каждом наблюдении. Например, массовый секундный расход топлива будет равен:

,

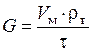где V_м– мерный объем, м³; ρ_т – плотность топлива, кг/м³; t – время, с.

В отличие от функциональной корреляционная зависимость проявляется приблизительно и лишь в массе наблюдений.

Примером корреляционной зависимости может служить общеизвестное соотношение между ростом человека и его весом. Оно записывается простейшим аналитическим выражением y = x –100, где у – вес человека в кг, а х – рост человека в см. Понятно, что для отдельного человека это соотношение может не соблюдаться, но для массы людей зависимость веса от роста в среднем будет определять некоторую «норму», отклонение от которой будет основанием для практических выводов.

Более сложный пример корреляционной зависимости: была предпринята попытка найти аналитическое выражение для расчета глубины наклепа в поверхностном слое деталей машин после обработки. По статистическим исследованиям глубина наклепа h_H описана экспериментальным уравнением следующего вида:

h_H = 12,28 × θ ^–1,4 × S ^0,14 × t ^0,11 × r ^0,1, мм,