Детерминированная модель управления запасами

Детерминированная модель управления запасами простейшего типа характеризуется постоянным во времени спросом, мгновенным пополнением запаса и отсутствием дефицита. Такую модель можно применять в следующих типичных ситуациях:

- использование некоторых промышленных изделий, таких как крепёжные элементы;

- использование осветительных ламп в здании;

- использование канцелярских товаров крупной фирмой;

- потребление основных продуктов питания.

На рис. 5.4 показано изменение уровня запаса во времени.

Предполагается, что интенсивность спроса (в единицу времени) равна b. Наивысшего уровня запас достигает в момент поставки заказа размером y (предполагается, что запаздывание поставки является заданной константой). Уровень запаса достигает нуля спустя у/b единиц времени после получения заказа размером у.

Рис. 5.4. Изменение уровня запаса во времени

Чем меньше размер заказа у, тем чаще нужно размещать заказы. Однако при этом средний уровень запаса будет уменьшаться. С другой стороны, с увеличением размера заказов уровень запаса повышается, но заказы размещаются реже (рис. 5.5).

Рис. 5.5. Частота размещения заказа

Так как затраты зависят от частоты размещения заказа и объема хранимого запаса, то величина у выбирается из условия обеспечения сбалансированности между двумя видами затрат. Это лежит в основе построения соответствующей модели управления запасами.

Пусть K – затраты на оформление заказа, имеющие место всякий раз при его размещении, h – затраты на хранение единицы заказа в единицу времени. Следовательно, суммарные затраты в единицу времени можно представить в виде

,

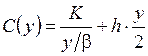где 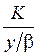– затраты на оформление заказа в единицу времени; 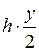– затраты на хранение запасов в единицу времени; t₀ = y/b – продолжительность цикла движения заказа; y/2 – средний уровень запаса.

Оптимальное значение у получается в результате минимизации С(у) по у. Таким образом, в предположении, что у – непрерывная переменная, имеем

,

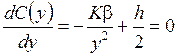оптимальный размер заказа определяется выражением

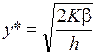. (5.4)

Данное выражение называют формулой экономичного размера заказа Уилсона. Можно доказать, что у* доставляет минимум С(у), показав, что вторая производная в точке у* строго положительна.

Таким образом, оптимальная стратегия модели предусматривает заказ у* единиц продукции через каждые t₀* = y*/b единиц времени. Оптимальные затраты в данном случае равны .

Для большинства реальных ситуаций существует положительный срок выполнения заказа (запаздывание) t_п от момента размещения заказа до его действительной поставки. Поэтому стратегия размещения заказов должна определять точку возобновления заказа (рис. 5.6).

Рис. 5.6. Положение точки размещения заказа

На рис. 5.6 показан случай, когда точка возобновления заказа должна опережать на t_пединиц времени ожидаемую поставку. Срок выполнения заказа t_пможно всегда принять меньше продолжительности цикла t₀*. В практических целях эту информацию можно просто преобразовать, определив точку возобновления заказа через уровень запаса, соответствующий моменту возобновлению. На практике это реализуется путем непрерывного контроля уровня запаса до момента достижения очередной точки возобновления заказа. Такую модель называют моделью непрерывного контроля состояния заказа.