Параметры качества математических моделей

К математическим моделям предъявляются основные требования универсальности, точности, адекватности, экономичности.

Универсальностьматематической модели характеризует полноту отражения в ней свойств реального объекта. Математическая модель отражают не все, а лишь некоторые свойства реального объекта. Например, формулы для сил резания не учитывают температуру окружающего воздуха, влажность, экономические параметры и т. д.

Точностьматематической модели оценивается степенью совпадения значений выходных параметров реального объекта и значений тех же параметров, рассчитанных с помощью модели.

Пусть отражаемые в математической модели свойства объекта оцениваются вектором выходных параметров Y = (y₁, y₂, … y_m). Тогда относительная погрешность математической модели E_i по i-му параметру равна:

,

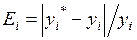где y_i^* – параметр, рассчитанный с помощью модели.

По этой формуле рассчитываются погрешности для каждого выходного параметра, в результате получается вектор погрешностей E = (E₁, E₂, … E_m). В целом для математической модели погрешность оценивается следующим образом:

.

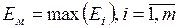Адекватностьматематической модели – это ее способность отражать заданные свойства объекта с погрешностью, не выше заданной.

В силу того, что выходные параметры модели являются функцией Y = F(X, Q) от параметров внутренних и входных, то и точность модели зависит от их значений. Адекватность модели имеет место в ограниченной области изменения внутренних и входных параметров. Если обозначить область адекватности как ОА, то

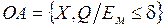
где d – некоторое заданное число.

Экономичностьматематической модели характеризуется затратами вычислительных ресурсов на ее реализацию. Если работа с математической моделью осуществляется вручную, то её экономичность определяется затратами личного времени проектировщика. Если модель используется при автоматизированном проектировании, то затратами машинного времени и памяти компьютера. Так как указанные величины определяются характеристиками конкретного компьютера, использовать их для оценки экономичности математической модели не вполне корректно. Поэтому, для оценки экономичности самой математической модели используют другие величины:

- среднее количество операций, выполняемых при одном обращении к математической модели;

- размерность системы уравнений в математической модели;

- количество используемых в модели внутренних параметров и т. д.

Требования высокой степени универсальности, точности, широкой области адекватности математической модели, с одной стороны, и высокой её экономичности, с другой стороны, противоречивы. Поэтому компромиссные решения определяются решаемой задачей.

Математические модели можно охарактеризовать и целым ряд других свойств, среди которых целесообразно выделить следующие:

- вычислимость – возможность ручного или с помощью ЭВМ исследования качественных и количественных закономерностей функционирования объекта (системы);

- модульность – соответствие конструкций модели структурным составляющим объекта (системы);

- алгоритмизируемость – возможность разработки соответсвующих алгоритма и программы, реализующей математическую модель на ЭВМ;

- наглядность – удобное визуальное восприятие модели.

- целенаправленность – модель всегда отображает некоторую систему, т. е. имеет цель;

- конечность – модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;

- упрощенность – модель отображает только существенные стороны объекта и, кроме того, должна быть проста для исследования или воспроизведения;

- доступность и технологичность для исследования или воспроизведения;

- информативность – модель должна содержать достаточную информацию о системе (в рамках гипотез, принятых при построении модели) и должна давать возможность получить новую информацию;

- сохранение информации, содержавшейся в оригинале (с точностью рассматриваемых при построении модели гипотез);

- полнота – в модели должны быть учтены все основные связи и отношения, необходимые для обеспечения цели моделирования;

- устойчивость – модель должна описывать и обеспечивать устойчивое поведение системы, если даже она вначале является неустойчивой;

- целостность – модель реализует некоторую систему (т. е. целое);

- замкнутость – модель учитывает и отображает замкнутую систему необходимых основных гипотез, связей и отношений;

- адаптивность – модель может быть приспособлена к различным входным параметрам, воздействиям окружения;

- управляемость (имитационность) – модель должна иметь хотя бы один параметр, изменениями которого можно имитировать поведение моделируемой системы в различных условиях;

- эволюционируемость – возможность развития моделей (предыдущего уровня).