Дифференциальных уравнений
РЕШЕНИЕ КРАЕВЫХ ЗАДАЧ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
Разработка и расчет новых изделий, аппаратов, конструкций или технологических процессов осуществляется на основе законов физики, механики, химии и т.д., которые обычно формулируются в виде дифференциальных уравнений. Математические модели многих, практически важных задач гидроаэромеханики, тепломассопереноса, теплопроводности, диффузии, теории упругости, задач на прочность, жесткость и устойчивость элементов конструкций и т.д. включают в свое описание дифференциальные уравнения в частных производных (их называют уравнениями математической физики). Решение большинства задач гидроаэромеханики, тепломассообмена, теории упругости и т.д. сводится к решению некоторых дифференциальных уравнений или системы дифференциальных уравнений. Например, расчет изгиба балки можно свести к решению краевой задачи для системы из двух обыкновенных дифференциальных уравнений второго порядка. Таким образом, любая задача проектирования, связанная с расчетом каких-либо конструкций, деталей, движения тел и т.д., в конечном счете, сводится к решению дифференциальных уравнений математических моделей. Для проведения вычислительного эксперимента на математической модели объекта исследования в силу ее сложности приходится использовать методы преобразования математической модели, например, методы линеаризации, дискретизации и т.д. Это существенно упрощает проведение вычислительного эксперимента на основе построенной математической модели.
Основные понятия, классификация, методы решения
дифференциальных уравнений
Дифференциальные уравнения в частных производных имеют бесконечное множество решений, т.к. их общее решение зависит от произвольных функций. При решении конкретной физической задачи необходимо из множества решений выбрать то, которое удовлетворяет некоторым дополнительным условиям. Такими дополнительными условиями чаще всего являются граничные условия (условия на границе заданной области) и начальные условия, относящиеся к моменту времени, с которого начинается исследуемый процесс. Совокупность граничных и начальных условий называется краевыми условиями. Нахождение решения дифференциального уравнения, удовлетворяющего начальным условиям (начальным данным), представляет собой задачу Коши. Задача нахождения решения дифференциального уравнения в некоторой области 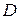 , удовлетворяющего на границе
, удовлетворяющего на границе 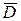 краевым условиям, является краевой задачей.
краевым условиям, является краевой задачей.
Для того чтобы решить математическую задачу (краевую задачу или задачу Коши) для каждого допустимого набора входных параметров, она должна быть корректно поставлена. Краевая задача называется корректно поставленной, если ее решение удовлетворяет следующим условиям: 1) решение существует; 2) решение единственно; 3) решение устойчиво, т.е. малым изменениям исходных данных соответствуют малые изменения решения (непрерывно зависит от исходных данных). Если хотя бы одно из этих условий не выполняется, то задача является некорректной. Для решения некорректно поставленных задач созданы специальные численные методы, получившие название методов регуляризации .
Для решения дифференциальных уравнений существуют аналитические и численные методы. Аналитические методы могут быть как точные (метод разделения переменных Фурье, метод функций Грина, и т.д.), так и приближенные (асимптотические, вариационные). Методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции. Аналитические методы полезны не только тем, что дают возможность получать точные решения. Они имеют также огромное значение для построения численных методов. Например, проверка разностных схем на известных решениях простейших уравнений позволяет оценить эти схемы, выяснить их сильные и слабые стороны. Получение точного решения математической задачи – это одна из основных целей исследования.
Для большинства дифференциальных уравнений, встречающихся при решении практических задач, не удается получить точного решения в виде аналитической функции. В таких случаях используют численные методы, которые представляют решение дифференциального уравнения в виде таблицы значений искомой функции в некоторых узловых точках с определенной точностью (конечно-разностные методы, конечных элементов). Интенсивное развитие и внедрение в практику математического моделирования вычислительных машин с большим быстродействием (суперкомпьютеров) повысили роль численных методов при решении различных задач математической физики. Стало возможным проводить многовариантные расчеты математических моделей сложных физических явлений, проектирования сложных конструкций, исследования в различных областях науки и практики.
Выбор соответствующего метода для решения дифференциального уравнения зависит от его вида. Классификация дифференциальных уравнений с частными производными нужна еще потому, что для каждого класса уравнений существует своя общая теория и общие методы решения. Классификация выполняется на основе следующих основных признаков:
1) порядка дифференциального уравнения;
2) количества независимых переменных;
3) линейности уравнения;
4) однородности уравнения;
5) вида коэффициентов дифференциального уравнения;
6) типа дифференциального уравнения.
Классы уравнений в соответствии с указанными выше признаками представлены в таблице:
| Признаки дифференциального уравнения | Классы дифференциальных уравнений | |||
| Порядок уравнения | Первого порядка | Старших порядков | ||
| Число переменных | Одна переменная Обыкновенное дифференциальное уравнение | Два и более переменных Уравнения в частных производных | ||
| Линейность уравнения | Линейные | Квазилинейные | Нелинейные | |
| Однородность уравнения | Однородные | Неоднородные | ||
| Вид коэффициентов | С постоянными коэффициентами | С переменными коэффициентами | ||
| Тип уравнения | Эллиптического типа | Гиперболического типа | Параболического типа | |
Обыкновенные дифференциальные уравнения. Общий вид обыкновенного дифференциального уравнения, устанавливающего связь между независимой переменной 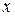 , неизвестной функцией
, неизвестной функцией 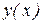 и ее производными
и ее производными 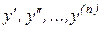 , может быть представлен в виде:
, может быть представлен в виде:
 . (7.1)
. (7.1)
Порядок наивысшей производной, входящей в уравнение, называется порядком этого уравнения. Решением дифференциального уравнения является некоторая функциональная зависимость 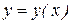 , которая при подстановке в уравнение обращает его в тождество. Общее решение дифференциального уравнения, которое формально определяется интегрированием, записывается в виде
, которая при подстановке в уравнение обращает его в тождество. Общее решение дифференциального уравнения, которое формально определяется интегрированием, записывается в виде 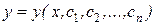 , где
, где 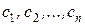 – произвольные постоянные интегрирования.
– произвольные постоянные интегрирования.
Решение, полученное из общего решения при фиксированных значениях 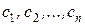 , называется частным решением уравнения. Постоянные интегрирования
, называется частным решением уравнения. Постоянные интегрирования 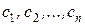 можно определить, если задать
можно определить, если задать 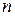 условий. Если эти условия задаются как совокупность значений искомой функции и всех ее производных до
условий. Если эти условия задаются как совокупность значений искомой функции и всех ее производных до 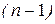 -го порядка включительно в некоторой точке
-го порядка включительно в некоторой точке 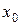 , то такая задача называется задачей Коши, а заданные условия:
, то такая задача называется задачей Коши, а заданные условия: 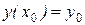 ,
, 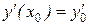 ,…,
,…, 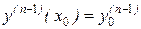 называются начальными условиями. Если же условия заданы на концах отрезка, где определяется решение, то задача называется краевой.
называются начальными условиями. Если же условия заданы на концах отрезка, где определяется решение, то задача называется краевой.
Дифференциальное уравнение (7.1) является линейным, если неизвестная функция 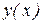 и все ее производные входят в уравнение только в первой степени (и не перемножаются друг с другом), в противном случае уравнение является нелинейным. Общий вид обыкновенного линейного дифференциального уравнения
и все ее производные входят в уравнение только в первой степени (и не перемножаются друг с другом), в противном случае уравнение является нелинейным. Общий вид обыкновенного линейного дифференциального уравнения 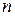 -го порядка имеет вид:
-го порядка имеет вид:
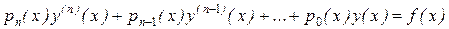 , (7.2)
, (7.2)
где 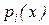 – известные функции независимой переменной
– известные функции независимой переменной 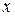 , называемые коэффициентами уравнения. Функция
, называемые коэффициентами уравнения. Функция 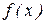 в правой части называется свободным членом. Если все коэффициенты уравнения (7.2) являются постоянными, т.е.
в правой части называется свободным членом. Если все коэффициенты уравнения (7.2) являются постоянными, т.е. 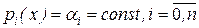 , то (7.2) является линейным дифференциальным уравнением с постоянными коэффициентами. Если уравнение (7.2) не содержит свободного члена,
, то (7.2) является линейным дифференциальным уравнением с постоянными коэффициентами. Если уравнение (7.2) не содержит свободного члена, 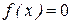 для всех значений независимой переменной, то оно является однородным дифференциальным уравнением. Для однородных дифференциальных уравнений выполняется принцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
для всех значений независимой переменной, то оно является однородным дифференциальным уравнением. Для однородных дифференциальных уравнений выполняется принцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
Простейшими дифференциальными уравнениями первого порядка, являются уравнения в полных дифференциалах, уравнения с разделяющимися переменными, однородные и линейные уравнения первого порядка, которые можно решить интегрированием и получить точное решение. Нелинейные дифференциальные уравнения в общем случае не имеют разработанных аналитических методов решения, кроме некоторых частных классов. Для получения общего решения неоднородного уравнения, зная общее решение однородного уравнения, без нахождения частного решения используется метод Лагранжа. В тех случаях, когда не удается получить точного решения обыкновенного дифференциального уравнения, применяются численные методы. Для численного решения задачи Коши можно использовать, например, методы Эйлера, Рунге-Кутта, Адамса и т.д. Для решения краевых задач часто применяют метод конечных разностей.
К числу важных обыкновенных дифференциальных уравнений, которые встречаются на практике, можно отнести: уравнение, описывающее второй закон Ньютона (классическая механика), уравнение Ван дер Поля (теория колебания), уравнение математического маятника, уравнения Бернулли, Риккати, Бесселя и т.д.
Дифференциальные уравнения в частных производных. Уравнение, связывающее искомую функцию 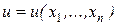 , независимые переменные
, независимые переменные 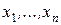 и частные производные от искомой функции, называется дифференциальным уравнением в частных производных:
и частные производные от искомой функции, называется дифференциальным уравнением в частных производных:
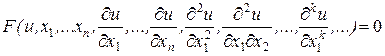 , (7.3)
, (7.3)
где 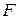 – заданная действительная функция точки
– заданная действительная функция точки 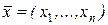 некоторой области
некоторой области 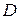 евклидова пространства
евклидова пространства 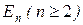 и действительных аргументов. Порядок старшей частной производной, входящей в уравнение (3.3) называется порядком уравнения. Уравнение (7.3) называется квазилинейным, если функция
и действительных аргументов. Порядок старшей частной производной, входящей в уравнение (3.3) называется порядком уравнения. Уравнение (7.3) называется квазилинейным, если функция 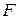 линейна относительно старших производных, а коэффициенты уравнения при старших производных зависят только от переменной
линейна относительно старших производных, а коэффициенты уравнения при старших производных зависят только от переменной 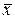 . Уравнение (7.3) называется линейным, если функция
. Уравнение (7.3) называется линейным, если функция 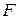 линейна относительно функции
линейна относительно функции 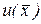 и ее производных, а коэффициенты уравнения зависят только от переменной
и ее производных, а коэффициенты уравнения зависят только от переменной 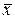 .
.
Многие практические задачи теплопроводности, диффузии, теории упругости и прочности и ряд задач из других областей описываются линейным дифференциальным уравнением в частных производных второго порядка, который можно записать в виде:
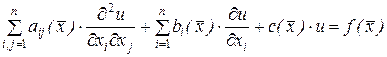 , (7.4)
, (7.4)
где 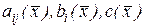 – коэффициенты дифференциального уравнения,
– коэффициенты дифференциального уравнения, 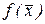 – свободный член. Все коэффициенты и свободный член дифференциального уравнения являются заданными функциями в области
– свободный член. Все коэффициенты и свободный член дифференциального уравнения являются заданными функциями в области 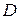 . Если
. Если 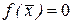 для всех
для всех 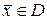 , то уравнение (7.4) называется однородным, в противном случае уравнение называется неоднородным. Если все коэффициенты уравнения являются постоянными, то уравнение (7.4) называется дифференциальным уравнением в частных производных с постоянными коэффициентами.
, то уравнение (7.4) называется однородным, в противном случае уравнение называется неоднородным. Если все коэффициенты уравнения являются постоянными, то уравнение (7.4) называется дифференциальным уравнением в частных производных с постоянными коэффициентами.
Для классификации дифференциальных уравнений в частных производных используют главную часть этих уравнений
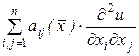
с дифференциальным оператором 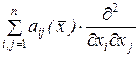 , который после формальной замены
, который после формальной замены 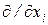 на
на 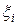 и
и 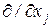 на
на 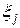 сводится к квадратичной форме следующего вида:
сводится к квадратичной форме следующего вида:
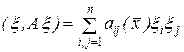
Матрица коэффициентов квадратичной формы является симметричной.
Для простоты рассмотрим уравнение с двумя независимыми переменными, т.е. 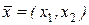 , (
, ( 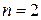 ). При фиксированном значении
). При фиксированном значении 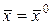 получаем уравнение
получаем уравнение
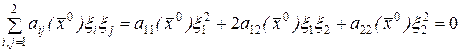 . (7.5)
. (7.5)
Это уравнение на плоскости 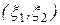 описывает некоторую кривую второго порядка. Тип кривой определяется знаком определителя
описывает некоторую кривую второго порядка. Тип кривой определяется знаком определителя
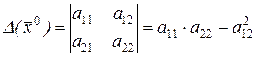 .
.
Возможны три различных случая при фиксированном значении 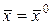 :
:
1) Определитель 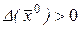 . В этом случае уравнение (7.5) является уравнением эллипса, а дифференциальное уравнение
. В этом случае уравнение (7.5) является уравнением эллипса, а дифференциальное уравнение
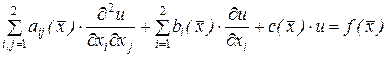 (7.6)
(7.6)
называется уравнение эллиптического типа (в точке 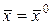 ).
).
2) Определитель 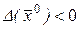 . Тогда уравнение (7.5) описывает гиперболу, а уравнение (7.6) называется уравнением гиперболического типа (в точке
. Тогда уравнение (7.5) описывает гиперболу, а уравнение (7.6) называется уравнением гиперболического типа (в точке 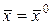 ).
).
3) Определитель 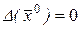 . В этом случае уравнение (7.5) будет уравнением параболы, а (7.6) – уравнением параболического типа (в точке
. В этом случае уравнение (7.5) будет уравнением параболы, а (7.6) – уравнением параболического типа (в точке 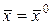 ).
).
Если уравнение (7.6) является эллиптическим, гиперболическим или параболическим в каждой точке области 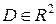 , то оно называется эллиптическим, гиперболическим или параболическим во всей области
, то оно называется эллиптическим, гиперболическим или параболическим во всей области 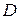 . Если Определитель
. Если Определитель 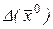 меняет знак в области
меняет знак в области 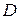 , то уравнение (7.6) – смешанного типа. Для классификации уравнений второго порядка при числе независимых переменных
, то уравнение (7.6) – смешанного типа. Для классификации уравнений второго порядка при числе независимых переменных 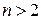 используется теория квадратичных форм. По каноническому виду квадратичной формы определяется тип дифференциального уравнения [44].
используется теория квадратичных форм. По каноническому виду квадратичной формы определяется тип дифференциального уравнения [44].
Рассмотрим несколько примеров:
1) Уравнение Пуассона (Лапласа)  – уравнение эллиптического типа (
– уравнение эллиптического типа ( 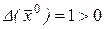 ).
).
2) Уравнение теплопроводности (диффузии) 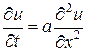 – уравнение параболического типа (
– уравнение параболического типа ( 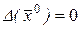 ).
).
3) Волновое уравнение 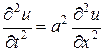 – уравнение гиперболического типа (
– уравнение гиперболического типа ( 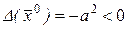 ).
).
Классические методы решения уравнений математической физики можно найти, например, в работе А. Н. Тихонова и А. А. Самарского [6]. Для решения уравнений математической физики обычно применяются методы разделения переменных, мгновенных источников, методы, основанные на применении функций Грина, Дирака и др. Эти классические методы предполагают отыскание, в первую очередь, общего решения и его последующее приспособление к частным условиям конкретной задачи. Также используются операционные методы, которые нашли применение в теплотехнике при решении разнообразных задач нестационарной теплопроводности, в химической технологии при решении задач нестационарной диффузии, при решении задач гидродинамики и др. Эффективными методами решения являются методы интегральных преобразований Лапласа, которые позволяют решать задачи без введения каких-либо новых допущений или преобразований, получать решения в форме, удобной для расчета.
При проведении вычислительного эксперимента математическая модель изучаемого объекта претерпевает ряд преобразований, необходимых для количественного анализа математической модели на вычислительной машине. Преобразования математической модели для количественного анализа непосредственно связаны с математическими методами. Для некоторых типов математических моделей без предварительных преобразований могут быть составлены алгоритмы численного решения, реализуемые на вычислительной машине. Например, математические модели в виде разностных уравнений, имитационные математические модели, являясь алгоритмическими математическими моделями, также не нуждаются в предварительном преобразовании перед реализацией на вычислительной машине. Часто имитационные математические модели используют в сочетании с методом статистических испытаний, методом Монте-Карло. Такой подход можно использовать и для решения дифференциальных уравнений с частными производными, если построить эквивалентную вспомогательную стохастическую математическую модель.
Краевой задаче, содержащей дифференциальные уравнения с частными производными и краевые условия, можно поставить в соответствие интегральную формулировку, т.е. можно представить в интегральной форме. При определенных условиях интегральную форму краевой задачи удается привести к вариационной формулировке минимизации некоторого функционала, который рассматривается на некотором множестве, содержащем искомую функцию. В этом случае говорят о вариационной форме модели. Для приближенного решения таких математических моделей, кроме приближенных аналитических вариационных методов Ритца, Бубнова-Галеркина, используется процедура метода конечных элементов (МКЭ), когда проводится дискретизация области конечными элементами и искомое решение приближенно представляется в виде линейной комбинации базисных функций. Для вычисления коэффициентов этой линейной комбинации необходимо решить систему линейных алгебраических уравнений относительно значений искомых функций в узлах конечных элементов.
Математические модели, содержащие в своем описании дифференциальные уравнения, могут быть достаточно сложными, нелинейными, в этом случае особое значение имеют методы линеаризации. Например, нелинейные модели разлагаются в ряд Тейлора и в первом приближении получаются линейные модели, а они достаточно хорошо изучены. Чтобы сделать возможным численное решение дифференциальных уравнений строится дискретная модель математической задачи, дифференциальные уравнения заменяются дискретными алгебраическими аппроксимациями и в результате этого получаются алгебраические системы уравнений. Наиболее удобными математическими моделями с точки зрения реализации на вычислительной машине являются линейные математические модели в виде системы линейных алгебраических уравнений. Поэтому многие математические методы, связанные с преобразованием математических моделей, ориентированы на последовательное сведение исходной математической модели к модели в виде системы линейных алгебраических уравнений.
Дата добавления: 2020-05-20; просмотров: 762;











