Устойчивость по перегрузке
Пусть самолет с фиксированным рулем высоты 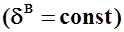 совершает квазиустановившийся криволинейный полет в вертикальной плоскости с постоянной скоростью и углом атаки. В этом случае коэффициент момента тангажа самолета равен:
совершает квазиустановившийся криволинейный полет в вертикальной плоскости с постоянной скоростью и углом атаки. В этом случае коэффициент момента тангажа самолета равен:
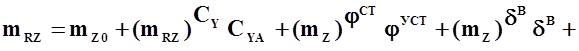 .
.
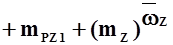 , (3.1)
, (3.1)
где 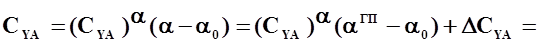
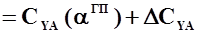 ;
;
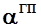 - угол атаки в установившемся горизонтальном полете с той же скоростью и на той же высоте, что и в криволинейном полете;
- угол атаки в установившемся горизонтальном полете с той же скоростью и на той же высоте, что и в криволинейном полете;
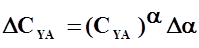 - коэффициент аэродинамической подъемной силы, искривляющей траекторию полета;
- коэффициент аэродинамической подъемной силы, искривляющей траекторию полета;
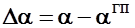 - приращение угла атаки в криволинейном полете по сравнению с углом атаки, обеспечивающим горизонтальный полет.
- приращение угла атаки в криволинейном полете по сравнению с углом атаки, обеспечивающим горизонтальный полет.
Найдем 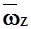 из условия равенства подъемной силы
из условия равенства подъемной силы 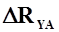 , искривляющей траекторию, и силы инерции
, искривляющей траекторию, и силы инерции 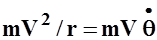 , возникающей в криволинейном движении:
, возникающей в криволинейном движении:
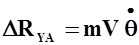 .
.
Здесь 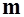 - масса самолета,
- масса самолета, 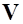 - его скорость,
- его скорость, 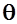 - угол наклона траектории,
- угол наклона траектории, 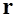 - радиус ее кривизны.
- радиус ее кривизны.
Величина 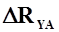 , обусловленная изменением только угла атаки, с учетом составляющей силы тяги равна:
, обусловленная изменением только угла атаки, с учетом составляющей силы тяги равна:
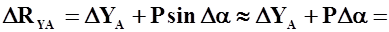
= 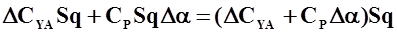 ,
,
где 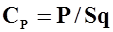 - коэффициент тяги.
- коэффициент тяги.
Поскольку 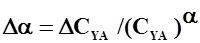 , то
, то
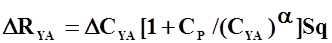 .
.
Дифференцируя по времени соотношение 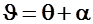 и имея в виду, что
и имея в виду, что  , получим
, получим
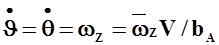 или
или 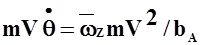 .
.
Следовательно, 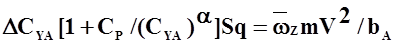 , откуда
, откуда
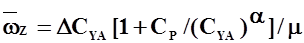 , (3.2)
, (3.2)
где 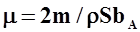 - относительная плотность самолета в продольном движении,
- относительная плотность самолета в продольном движении, 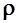 - плотность атмосферы.
- плотность атмосферы.
Выражение для 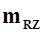 принимает вид
принимает вид
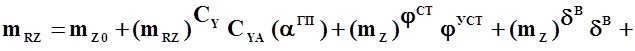 .
.
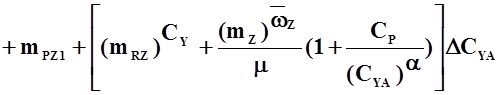 . (3.3)
. (3.3)
Так как опорное движение (установившийся горизонтальный полет) сбалансировано, то при 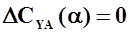 :
:
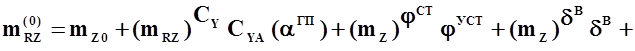
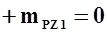 .
.
Следовательно,
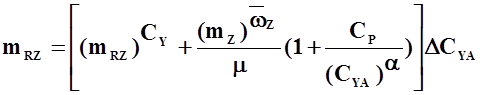 . (3.4)
. (3.4)
Возьмем полную производную от 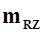 по
по 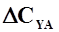 при
при 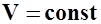 и обозначим ее через
и обозначим ее через 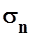 :
:
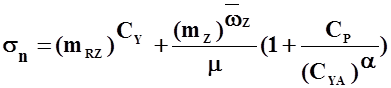 . (3.5)
. (3.5)
Имея ввиду, что 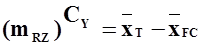 , получим
, получим
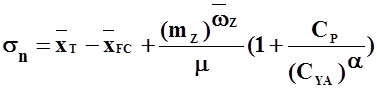 . (3.6)
. (3.6)
Полная производная 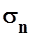 коэффициента момента тангажа по коэффициенту подъемной силы при фиксированном руле высоты в квазиустановившемся криволинейном движении самолета в вертикальной плоскости с постоянной скоростью называется степенью продольной статической устойчивости по перегрузке при фиксированном руле высоты.
коэффициента момента тангажа по коэффициенту подъемной силы при фиксированном руле высоты в квазиустановившемся криволинейном движении самолета в вертикальной плоскости с постоянной скоростью называется степенью продольной статической устойчивости по перегрузке при фиксированном руле высоты.
Если 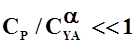 , а
, а 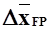 мало по сравнению с
мало по сравнению с 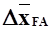 , то можно принимать
, то можно принимать
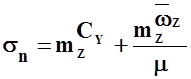 , (3.7)
, (3.7)
где 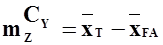 .
.
По знаку производной 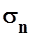 можно судить о продольной статической устойчивости по перегрузке. Величина и знак производной определяются по формулам или по тангенсу угла наклона кривой
можно судить о продольной статической устойчивости по перегрузке. Величина и знак производной определяются по формулам или по тангенсу угла наклона кривой 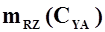 в точке, соответствующей режиму балансировки
в точке, соответствующей режиму балансировки 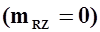 .
.
Дата добавления: 2016-06-29; просмотров: 2487;











