Задача о влиянии ледникового периода на геотерму

Моделирование геотермического распределения с учетом переменной температуры на поверхности Земли

Рассмотрим более общий случай, когда температура на поверхности Земли изменяется во времени, т.е. случай когда температура на поверхности Земли представлена какой-то зависимостью от времени φ(t).

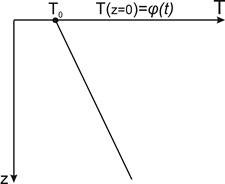
Рис. 3.4 Начальное распределение температуры среды

Допущения: Земля – однородное полупространство. Одномерный теплоперенос путем теплопроводности. Распределенных источников тепла нет.

Тогда математическая постановка задачи имеет вид:

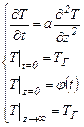, (3.36)

здесь T_Г=T₀+Гz.

Данная задача решается аналитически. Сначала введем новую функцию u(z,t)=T(z,t)-T_Г(z), величину нарушения геотермы.

Постановка задачи для u(z,t) принимает вид

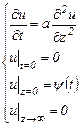, (3.37)

здесь ψ(t)=φ(t)-T₀.

Для решения используем теорему Дьюамеля. Если нам известно решение Ф(z,t) задачи (3.37) для u(z=0)=1, то решение задачи (3.37) для u(z=0)=ψ(t) по теореме Дьюамеля будет

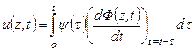. (3.38)

Поскольку

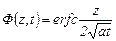, (3.39)

то

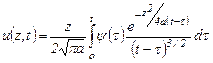. (3.40)

Возвращаясь к T(z,t) имеем для температуры среды при переменной температуре на поверхности

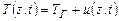. (3.41)

Задача о влиянии ледникового периода на геотерму

Последний ледниковый период начался 13 тыс. лет назад и длился 7 тыс. лет. В ледниковый период температура поверхности Земли охладилась на 20 градусов.

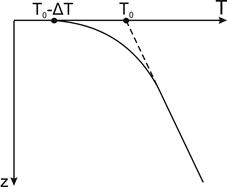
Рис. 3.5. Геотерма в конце ледникового период

В результате длительно поддержания низкой температуры на поверхности Земли геотерма нарушилась для z>0.

При оценке последствий последнего ледникового периода на распределении температуры в недрах Земли нас интересует промежуток времени после окончания ледникового периода (если момент окончания последнего ледникового периода обозначить, как θ, то нас интересует время t>θ)

Согласно (3.40) нарушение геотермы в конце ледникового периода

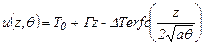(3.42)

Для t>θ задача решается аналитически. Для этого воспользуемся формулой (3.41). Решим методом линейной суперпозиции.

Предположим, что на поверхности и для t>θ поддерживается температура T₀-ΔT, а поскольку для t>θ температура поверхности вернулась к прежнему значению T₀ добавим новую температуру поверхности T₀+ΔT. Таким образом, для t>θ будем считать, что на поверхности Земли продолжается поддерживаться старая температура ΔT ниже и с момента t=θ начинается поддерживаться новая температура на ΔT выше. В сумме они дают возврат к температуре T₀.

Решение имеет вид

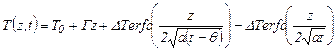. (3.43)

Используя (3.43) можно оценить последствия последнего ледникового периода на распределение температуры в недрах Земли в настоящее время.

Схематически распределение температуры согласно (3.43) имеет вид

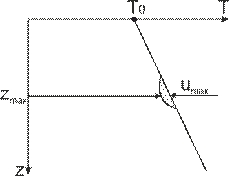
Рис. 3.6. Нарушенная геотерма

На глубине z_max должна наблюдаться максимальная величина нарушения геотермы u_max.