Моделирование геотермического распределения с учетом изменения температуры на поверхности по гармоническому закону.

В природе многие процессы периодические. Например есть колебания температуры воздуха с периодом 1 сутки, ночью в среднем холоднее, днем – теплее. Есть сезонные колебания с периодом 1 год.

Любые периодические изменения температуры на поверхности можно представить как серию гармонических колебаний с одинаковой частотой, но с различными амплитудами и сдвигами по фазе. Чтобы описать влияние на геотерму колебаний температуры на поверхности Земли по гармоническому закону, рассмотрим следующую задачу

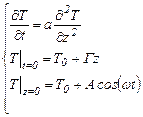. (3.44)

Здесь

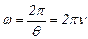. (3.45)

θ – период колебаний, ν – частота.

Данная задача решается аналитически. Воспользуемся решением для произвольной переменной температуры поверхности (3.41). Подставим ψ(t)=Acosωt (3.41). Получим для больших времен (t→∞)

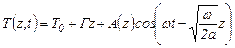. (3.46)

Из (3.46) следует, что установившиеся колебания температуры на глубине z совершаются с той же частотой ω, но они сдвинуты по фазе относительно колебаний температуры на поверхности.

Амплитуда колебаний убывает с глубиной по экспоненциальному закону

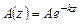(3.47)

или

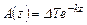, (3.48)

Здесь

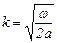. (3.49)

Тогда видно, что решение (3.46) представляет собой уравнение волны.

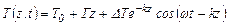(3.50)

Графиком данного решения будет геотерма в виде волны, амплитуда которой угасает по мере увеличения глубины.

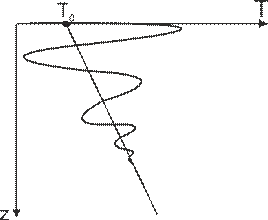
Рис. 3.7. Нарушенная геотерма