Десятичные дроби. Примеры

Десятичная система исчисления основана на цифрах от 0 до 9. Число типа 53.17 — десятичная дробь, точка отделяет целую часть 53 от дробной части 0.17.

Число, которое может быть точно выражено в виде десятичной дроби, называют конечной десятичной дробью, а число, которое не может быть точно выражено в виде десятичной дроби, - бесконечной десятичной дробью. Таким образом, 3/2 = 1.5 — это конечная десятичная дробь, а 4/3 = 1.33333... — бесконечная десятичная дробь. Число 1.33333... можно записать в виде 1.3(3), т. е. «одна целая, три в периоде».

В зависимости от требуемой точности бесконечная десятичная дробь может быть записана двумя способами: (1) с точностью до некоторого количества значащих цифр, т. е. цифр, которые что-то означают, и (2) с точностью до определенного десятичного разряда, т. е. определенного количества знаков после десятичной точки.

Цифра последнего десятичного разряда в ответе не меняется, если справа за ней стоит цифра 0, 1, 2, 3 или 4; и она увеличивается на 1, если справа стоит цифра 5, 6, 7, 8 или 9. Таким образом, бесконечная дробь 7.6183 при округлении до третьей значащей цифры превращается в 7.62, так как дальше справа стоит цифра 8, принадлежащая группе 5, 6, 7, 8, 9. При округлении до третьего десятичного разряда 7.6183 превращается в 7.618, поскольку справа от цифры 8 стоит цифра 3.

Пример. Вычислить 42.7 + 3.04 + 8.7 + 0.06.

Запишем числа таким образом, чтобы точки находились друг под другом. Будем складывать числа в каждом столбце и начнем справа:

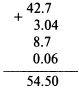
В результате получаем 42.7 + 3.04 + 8.7 + 0.06 = 54.50.

Пример. Вычислить 74.3 х 3.8.

При умножении десятичных дробей числа перемножаются так, как если бы они были целыми, т. е.

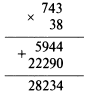
Положение десятичной точки определяется общим количеством знаков справа после десятичной точки в обоих сомножителях. Здесь в двух перемножаемых числах (1 + 1) = 2 знака после десятичной точки (74.3 х 3.8).

Следовательно, 74.3 х 3.8 = 282.34.

Пример. Вычислить 37.81 : 1.7 с точностью до 4 значащих цифр и 4 десятичного разряда.

Умножаем знаменатель на 10. Умножаем также числитель на 10, чтобы сохранить значение дроби. Получаем в знаменателе целое число, т. е. 37.81 : 1.7 = 37 х 10/1.7 х 10 = 378.1/17.

Деление в столбик десятичных дробей аналогично делению в столбик целых чисел, поэтому покажем только первые четыре шага:

Итак, 37.81:1.7 = 22.24 с точностью до 4 значащих цифр;

37.81:1.7 = 22.2412 с точностью до 4 десятичного разряда.

Пример. Преобразовать 0.4375 в правильную дробь. Дробь 0.4375 можно без изменения ее значения записать виде

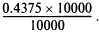
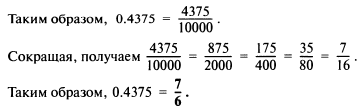
Для преобразования правильной дроби в десятичную надо разделить числитель на знаменатель.

Пример. Выразить 9/16 в виде десятичной дроби.

Деление на 16 можно осуществить в столбик, а можно просто сократить дробь на 2 (9/2 = 4.50), потом на 8 (4.50/8 = 0.5625).

Итак, 9/16 = 0.5625.