Десятичные и двоичные числа
Повседневно применяемая система чисел является десятичной, в ней используются цифры от 0 до 9. Система имеет десять разных разрядов (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9), и говорят, что ее основание равно 10.
Двоичная система счисления имеет основание 2 и использует только цифры 1 и 0.
Преобразование двоичных чисел в десятичные. Десятичное число 234.5 эквивалентно числу
2 х 102 + 3x 101 + 4 х 100 + 5 х 10-1
или сумме членов, каждый из которых содержит цифру, умноженную на основание, возведенное в некоторую степень.
У двоичной системы счисления основание 2, значит, число 1101.1 эквивалентно 1 х 23 + 1 х 22 + 0 х 21 + 1 х 20 + 1 х 2-1.
Таким образом, эквивалентное двоичному числу 1101.1 десятичное число равно 8 + 4 + 0 + 1 + 1/2, т. е. 13.5. Итак, 1101.12 = 13.510, индексы 2 и 10 означают двоичную и десятичную системы счисления соответственно.
Пример. Преобразовать 101.01012 в десятичное число.
101.01012 = 1 х 22 + 0 х 21 + 1 х 20 + 0 х 2-1 + 1 х 2-2 + 0 х 2-3 + 1 х 2-4 = 4 + 0 + 1 + 0 + 0.25 + 0 + 0.0625 = 5.312510.
Преобразование десятичных чисел в двоичные. Целое десятичное число может быть преобразовано в соответствующее ему двоичное число посредством последовательного деления на 2 и записи остатка на каждом этапе деления, как показано ниже на примере числа 3910.
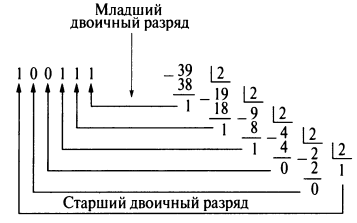
В искомом результате цифру старшего разряда остатка записывают как младший двоичный разряд (бит — это двоичный разряд, а младший разряд — тот, что находится справа). Младший бит остатка — это старший разряд, т. е. бит слева. Таким образом, 3910 = 1001112.
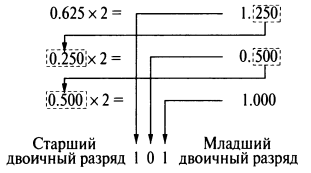
Для дробей старший разряд результата — это старший бит целой части произведения исходного числа на 2. Младший разряд результата — это младший бит целой части произведения исходного числа на 2. Таким образом, 0.62510 = 0.1012.
Преобразование десятичного числа в двоичное через десятичное. Для целых десятичных чисел, содержащих несколько разрядов, последовательное деление на 2 может быть длительным процессом. В данном случае, как правило, проще преобразовать десятичное число в двоичное через восьмеричную систему счисления. Эта система имеет основание 8 и использует цифры 0,1,2, 3, 4, 5, 6 и 7. Десятичное число, эквивалентное числу 43178, — это
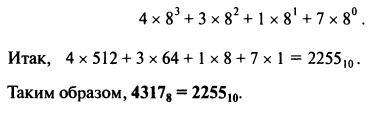
Целое десятичное число может быть преобразовано в соответствующее ему восьмеричное число посредством последовательного деления на 8 и записи остатка на каждом этапе деления, как показано ниже на примере числа 49310.
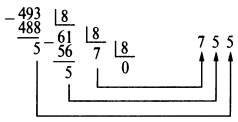
Таким образом, 49310 = 7558.
Дробная часть десятичного числа может быть преобразована в восьмеричную систему посредством умножения на 8, как показано ниже на примере дроби 0.437510:
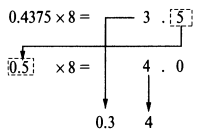
Для дробей старший разряд — это старший разряд числа, полученного при умножении дроби на 8. Итак
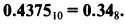
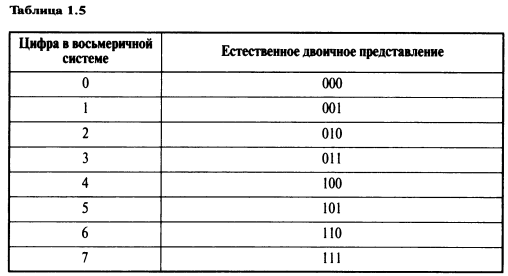
Естественное двоичное представление для цифр от 0 до 7 показано в Табл. 1.5. Восьмеричное число может быть преобразовано в двоичное посредством записи трех разрядов, соответствующих цифре в восьмеричной системе. Таким образом
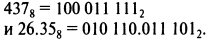
Если в старшем разряде записан «0», он не означает ничего. Таким образом
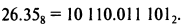
Чтобы преобразовать 11 110 011.100 012 в десятичное число через восьмеричную систему, поступаем так.
Группируем двоичные цифры в группы по три по правилам двоичной системы:

Используя Табл. 1.5 для преобразования этого двоичного числа в восьмеричное, в итоге получаем 363.428, откуда
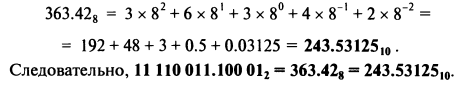
Дата добавления: 2025-01-25; просмотров: 297;











