Свойства четырехугольников
Многоугольник — это замкнутая фигура, ограниченная прямыми линиями. Многоугольник, имеющий:
- 3 стороны, называется треугольником,
- 4 стороны, называется четырехугольником,
- 5 сторон, называется пятиугольником,
- 6 сторон, называется шестиугольником,
- 7 сторон, называется семиугольником,
- 8 сторон, называется восьмиугольником.
Существует пять типов четырехугольников, а именно:
- прямоугольник,
- квадрат,
- параллелограмм,
- ром6,
- трапеция.
Их свойства рассмотрены далее.
Если противолежащие углы любого четырехугольника соединить прямой линией, получится два треугольника. Поскольку сумма углов треугольника равняется 180°, сумма углов четырехугольника равняется 360°.
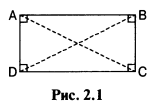
В прямоугольнике, показанном на Рис. 2.1:
- все четыре угла — прямые,
- противоположные стороны параллельны и равны по длине,
- диагонали АС и BD равны по длине и в точке пересечения делят друг друга пополам.
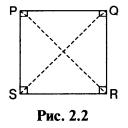
В квадрате, показанном на Рис. 2.2:
- все четыре угла — прямые,
- противоположные стороны параллельны,
- все четыре стороны равны по длине
- диагонали PR и QS равны по длине и пересекаются под прямым углом, в точке пересечения деля друг друга пополам.
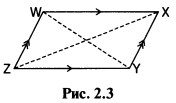
В параллелограмме, показанном на Рис. 2.3:
- противолежащие углы равны,
- противоположные стороны параллельны и равны по длине,
- диагонали WY и XZ в точке пересечения делят друг друга пополам.
В ромбе, показанном на Рис. 2.4:
- противолежащие углы равны,
- противолежащие углы делятся диагоналями пополам,
- противоположные стороны параллельны,
- все четыре стороны равны по длине,
- диагонали АС и BD пересекаются под прямым углом и в точке пересечения делят друг друга пополам.


В трапеции, показанной на Рис. 2.5, только две стороны параллельны.
Площади подобных фигур. Площади подобных фигур пропорциональны квадратам соответствующих линейных размеров. Например, на Рис. 2.11 представлены два квадрата, сторона одного из которых в 3 раза больше стороны другого.
Площадь фигуры на Рис. 2.11а равна (х)(х) = х2.
Площадь фигуры на Рис. 2.116 равна (3х)(3х) = 9x2.
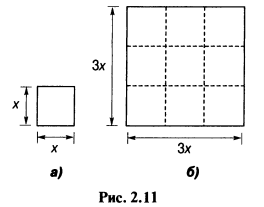
Следовательно, площадь фигуры на Рис. 2.11б в (З)2 раз больше, чем площадь фигуры на Рис. 2.11а.
Пример. Прямоугольный гараж на плане здания имеет размеры 10 на 20 мм. Если план нарисован в масштабе 1 к 250, истинные размеры гаража можно определить следующим образом.
Вычислим площадь гаража на плане: 10 мм х 20 мм = 200 мм2.
Поскольку площади подобных фигур пропорциональны квадратам соответствующих линейных размеров, то истинная площадь гаража
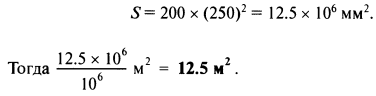
Дата добавления: 2025-01-25; просмотров: 462;











