Техника умножения епюр по правилу

Верещагина

Эпюры изгибающих моментов в действительном состоянии балки, в зависимости от нагрузки, могут быть ограничены кривыми линиями (чаще всего квадратичной параболой, или ее частью), а также прямыми линиями.

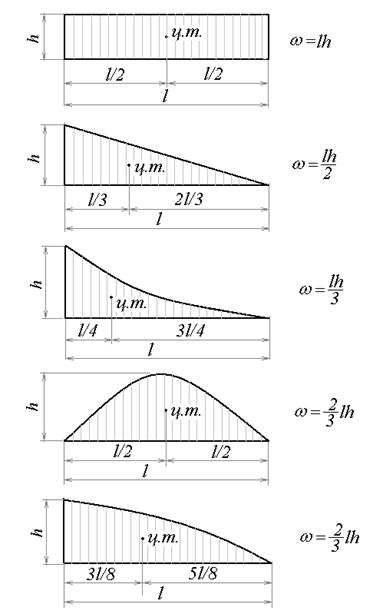
Рис.11.27

Поэтому на любом участке балки эпюра изгибающих моментов может состоять из следующих простых фигур: прямоугольника, треугольника, вогнутой квадратичной параболы (или её половины), выгнутой квадратичной параболы (или её половины). На рис.11.27 приведены формулы для определения площадей этих фигур и координаты центров тяжести. Если на каком-то участке эпюра имеет форму трапеции, то ее легко разделить на два треугольника и рассматривать каждый из них отдельно при выполнении процесса перемножения эпюр.

Эпюры изгибающих моментов в единичном (возможном) состоянии балки всегда имеют прямолинейную форму на любом участке балки, то есть форму прямоугольника, треугольника или трапеции. При определении ординат этих фигур под центрами тяжести какой-либо фигуры действительного состояния используем соотношение между координатами центров тяжести и длинами участков.

Рассмотрим общий случай, когда на каком-то участке действительного состояния эпюра изгибающих моментов криволинейная и на концах участка имеет ординаты h₁и h₂, а эпюра изгибающих моментов единичного состояния на этом участке имеет форму трапеции с ординатами b₁и b₂. Обозначим длину участка через а(рис.11.28). Чтобы перемножить эти эпюры по правилу Верещагина, разделим первую епюру (в заданном состоянии) на три фигуры: квадратичную параболу 1 и два треугольника 2 и 3.

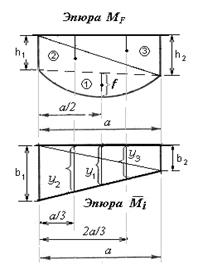
Рис.11.28

Как видно из рисунка 11.28 все простые фигуры имеют общее основание, равноеа, и разные высоты. Используя известные формулы (рис.11.27), определяем площади трех фигур действительного состояния балки: ω₁=2/3a 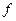; ω₂=1/2ah₁; ω₃=1/2ah₂.Координаты центров тяжести этих фигур известны, они приведены на рис. 11.28.

Определим ординаты эпюры единичного состояния под центрами тяжести каждой части эпюры действительного состояния, используя соотношение расстояний центров тяжести от начала и конца участка к длине участка. Эти ординаты соответственно равняются:

y₁ =1/2(b₁+ b₂); y₂ =2/3b₁+1/3b₂; y₃ =1/3b₁+2/3 b₂.

Перемножим площади отдельных частей эпюры заданного состояния на соответствующие ординаты эпюры единичного состояния и найдем сумму этих величин. Тогда получим общую формулу умножения этих эпюр по правилу Верещагина:

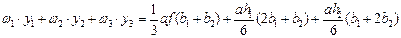, или

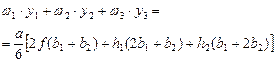(11.65)

Формула (11.65) применяется в любом случае, то есть при любых значениях ординат 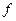, h₁, h₂, b₁, и b₂ (положительных, отрицательных, или нулевых).

При перемножении эпюр изгибающих моментов с использованием формулы (11.65) нужно разделить эпюры изгибающих моментов на простые фигуры в пределах каждого участка, определить в действительном состоянии площади этих фигур и положения их центров тяжести, а также найти ординаты эпюры в единичном состоянии под центрами тяжести эпюры действительного состояния.

Для определения перемещения необходимо разделить величину, найденную по формуле (11.65) на жесткость соответствующего участка балки.

Задание 11.1 для самостоятельной работы: Для заданных расчетных схем балок построить эпюры поперечных сил и изгибающих моментов и определить размеры поперечных сечений двутавровой формы из условия прочности, если расчетное сопротивление равняется 210 МПа.

Балка 1.

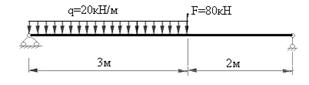
Балка 2.

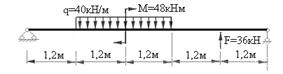
Балка 3.

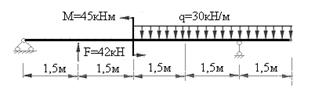
Балка 4.

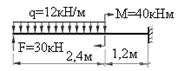
Балка 5.

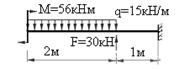
Задание 11.2 для самостоятельной работы: Построить эпюры прогибов и углов поворота для балок 1 и 5.

Задание 11.3 для самостоятельной работы: Определить прогиб и угол поворота правого торца балки 3 и левого торца балки 4, пользуясь правилом Верещагина.