Касательные напряжения в поперечном сечении вала

При определении напряжений в поперечном сечении вала круглой формы принимаются следующие предположения (допущения):

1) Поперечные сечения вала, которые до деформации были плоскими и нормальными к его оси, остаются плоскими и нормальными к оси вала после деформации (гипотеза плоских сечений при кручении). Плоские сечения получают повороты на некоторые углы вокруг оси вала;

2) Радиусы поперечных сечений вала остаются прямыми (не искривляются) и сохраняют свою начальную длину;

3) Образующие цилиндрической поверхности вала остается прямыми после его деформации;

4) Расстояния между поперечными сечениями вала при кручении не изменяются.

Формулы определения напряжений и деформаций, которые будут доказаны с использованием этих предположений, совпадают с формулами точного метода теории упругости и подтверждаются опытным путем.

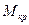Рассмотрим один участок прямого вала длиной . Поперечное сечение вала имеет круглую форму радиуса r. Допустим, что крутящий момент в произвольном поперечном сечении этого участка известен и равняется с положительным знаком. Это означает, что на торцах этого участка действуют моменты 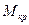, направленные против часовой стрелки относительно внешних нормалей, проведенных к торцевым сечениям рассматриваемого участка вала (рис.12.3).

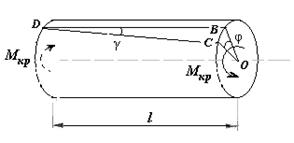
Рис.12.3

Закрепим условно левый торец участка и проведем некоторую образующую DB цилиндрической поверхности вала и радиус правого торца BO. Тогда правый торец вернется относительно левого на угол φ, а образующая вернется относительно своего первоначального состояния на угол γ и займет положение DC, оставшись прямолинейной. Угол φ называется полным углом закручивания на участке длиной 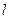, а угол γ является относительным углом сдвига.

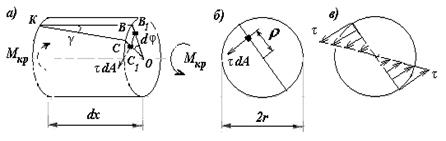
Рис.12.4

Отсечем от правого торца рассмотренного участка вала ее элемент длиной dx (рис.12.4,а). Крутящий момент, который действует в плоскости правого торца, условно вынесем за его пределы, чтобы он не мешал использованию необходимых обозначений в этой плоскости. Закрепим левый торец отсеченного элемента вала.Тогда его правый торец повернется в направлении действия крутящего момента на некоторый элементарный угол dφотносительно левого торца. На такой же угол вернется радиус ОВ и займет положение ОС. При этом образующая КВ повернется на угол γ и займет положение КС. В пределах малых деформаций дугу ВС можно заменить хордой и найти зависимость между γ и dφ. Из треугольника ВОС имеем ВС = r· dφ, а из треугольника КВС - ВС = γ· dx,откуда получим:

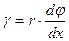(12.5)

Таким образом, угол сдвига волокна КВ, расположенного на поверхности элемента вала, пропорциональный радиусу поперечного сечения r и относительному углу закручивания dφ/ dx.

Зависимость (12.5) сохранится для произвольного продольного волокна, взятого на расстоянии ρ от центра круглого сечения, то есть волокна, которое выходит из точки В₁ и расположено параллельно волокну КВ. В этом случае в зависимости (12.5) нужно заменить r на ρ. В результате получим:

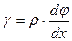(12.6)

От действия крутящего момента в каждой точке поперечного сечения возникают касательные напряжения τ. Эти напряжения расположены в плоскости сечения и имеют разные значения для разных точек этого сечения. Выделим вокруг точки В₁ элементарную часть площади сечения и обозначим ее через dA. Эта часть площади повернется на угол dφот действия крутящего момента и займет положение С₁. Равнодействующая касательных напряжений, которые действуют на элементарную площадь dA в точке С₁ будет равняться произведению τ·dA и эта сила всегда направлена перпендикулярно радиусу точки С₁ в направлении действия крутящего момента.

Элементарный момент равнодействующей касательных напряжений относительно оси вала равняется произведению ρ·τ·dA. Ввиду того, что в плоскости сечения действует безгранично большое количество таких элементарных моментов и их сумма равняется крутящему моменту, найдем статическую зависимость между касательным напряжением и крутящим моментом в интегральной форме:

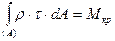(12.7)

Используем, наконец, известную физическую зависимость между углом сдвига и касательным напряжением (закон Гука при сдвиге):

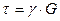(12.8)

Заменим в формуле (12.8) угол γ его значением согласно зависимости (12.6) и подставим в интеграл (12.7). В результате получим:

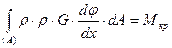, или 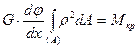, откуда

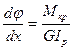(12.9)

Таким образом, относительный угол закручивания прямо пропорциональный крутящему моменту и обратно пропорциональный жесткости поперечного сечения вала при кручении, то есть величине .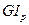

Найдем касательные напряжения из зависимости (12.8) с учетом зависимостей (12.6) и (12.9):

,

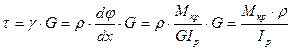окончательно 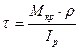(12.10)

То есть, касательные напряжения линейно увеличиваются от центра поперечного сечения вала к его поверхности. На рис.12.4,в изображена эпюра касательных напряжений вдоль диаметра круглого сечения. Максимальные касательные напряжения возникают в точках сечения, которые больше всего удалены от центра, то есть при ρ = r. При этом:

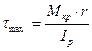, или 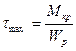(12.11)

где 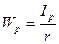является полярным моментом сопротивления поперечного сечения. Для сечения круглой формы он определяется по формуле: 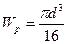(12.12)

Выводы: 1) Для доказательства формулы касательных напряжений, которые возникают в поперечном сечении вала нужно рассматривать три аспекта задачи: геометрический, статический и физический.

Рассматривая геометрическую схему деформаций элемента бруса длиной dx, устанавливаем зависимости (12.5) и (12.6) между углом сдвига и элементарным углом закручивания.

Рассматривая действие касательного напряжения на элементарную площадку dA сечения, устанавливаем статическую зависимость (12.7).

Физическую зависимость (12.8) используем из темы «сдвиг».

2) Касательные напряжения в произвольной точке сечения линейно зависят от расстояния этой точкой до центра сечения. В центре сечения касательные напряжения равняются нулю, а в точках, которые близко расположены вокруг центра сечения, касательные напряжения имеют небольшие значения. Это означает, что центральная часть сечения вала не используется или почти не влияет на прочность вала. Поэтому целесообразно принимать пустотелые сечения вала, которые имеют внешний диаметр D и внутренний диаметр d (примером может быть толстостенная труба). Момент сопротивления такого сечения определяется последующей формуле:

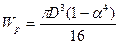, где 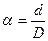(12.13)