Вынужденные гармонические колебания в колебательном контуре. Резонанс. Резонансные кривые для заряда конденсатора и силы тока в контуре.

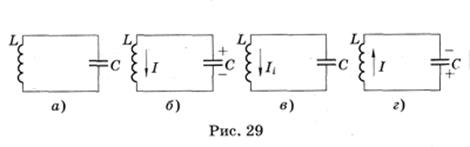
Электромагнитные колебания — это колебания электрического и магнитного полей, которые сопровождаются периодическим изменением заряда, силы тока и напряжения. Простейшей системой, где могут возникнуть и существовать свободные электромагнитные колебания, является колебательный контур. Колебательный контур — это цепь, состоящая из катушки индуктивности и конденсатора (рис. 29, а). Если конденсатор зарядить и замкнуть на катушку, то по катушке потечет ток (рис. 29, б). Когда конденсатор разрядится, ток в цепи не прекратится из-за самоиндукции в катушке. Индукционный ток, в соответствии с правилом ленца, будет иметь то же направление и перезарядит конденсатор (рис. 29, в). Процесс будет повторяться (рис. 29, г) по аналогии с колебаниями маятниками. Таким образом, в колебательном контуре будут происходить электромагнитные колебания из-за превращения энергии электрического поля конденсатора ( 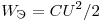) в энергию магнитного поля катушки с током ( 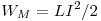), и наоборот. Период электромагнитных колебаний в идеальном колебательном контуре (т. Е. В таком контуре, где нет потерь энергии) зависит от индуктивности катушки и емкости конденсатора и находится по формуле томсона 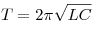. Частота с периодом связана обратно пропорциональной зависимостью .

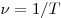В реальном колебательном контуре свободные электромагнитные колебания будут затухающими из-за потерь энергии на нагревание проводов. Для практического применения важно получить незатухающие электромагнитные колебания, а для этого необходимо колебательный контур пополнять электроэнергией, чтобы скомпенсировать потери энергии. Для получения незатухающих электромагнитных колебаний применяют индукционный генератор.

Согласно закону электромагнитной индукции, в нем возникает эдс с частотой 50 гц, изменяющаяся по гармоническому закону .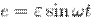

Под действием эдс и идет переменный ток с частотой 50 гц во всех лампочках, холодильниках и стиральных машинах в квартирах.

Переменный ток — это вынужденные электромагнитные колебания. Действительно, если ток изменится по гармоническому закону 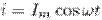, то его магнитное поле также совершает гармоническое колебание с частотой 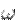. Причина тока — электрическое поле. Следовательно, с такой же частотой меняется электрическое поле в проводнике.

Явление резонанса заключается в том, что амплитуда установившихся вынужденных колебаний достигает наибольшего значения, когда частота вынуждающей силы равна собственной частоте колебательной системы.

Если активное сопротивление r в колебательном контуре мало, то, по аналогии с механической колебательной системой с малым коэффициентом трения μ, в нем возможен вполне отчетливый резонанс (рис. 3.71).

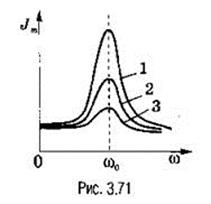
Сила тока при вынужденных колебаниях в контуре достигнет максимального значения, когда частота вынуждающих колебаний ω (частота приложенного к контуру переменного напряжения) сравняется с собственной частотой электрического колебательного контура ω0:

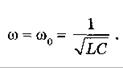
Амплитуда установившихся колебаний силы тока при резонансе равна:

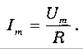
При r → 0 резонансное значение силы тока неограниченно возрастает:

(im) рез→∞. Наоборот, при больших r говорить о резонансе не имеет смысла. Зависимости амплитуды силы тока от частоты (резонансные кривые) представлены на рис. 3.71. Они подобны резонансным кривым колебаний пружинного маятника (рис. 1.63), где хm = im, а номерам кривых 1, 2, 3 соответствуют сопротивления контура r1 < r2 < r3.

Амплитуда напряжения при резонансе растет одновременно с ростом силы тока. Напряжения на конденсаторе и катушке индуктивности становятся одинаковыми и во много раз превосходят внешнее напряжение. Так как

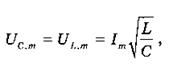
А внешнее напряжение связано с резонансным током соотношением um = im r, то при 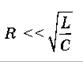получим:

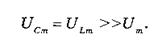
Волны, виды волн. Основные понятия (характеристики волны). Механические волны. Уравнение плоской волны, распространяющейся вдоль оси х. Уравнение плоской волны, распространяющейся в произвольном направлении. Уравнение сферической волны. Энергия механических волн, поток энергии, плотность потока энергии. Вектор умова.

Волны, виды волн.

Волна– процесс распространения колебаний в упругой среде.

Виды волн:

1. Продольные – частицы среды совершают колебания по направлению распространения волны – во всех упругих средах;

Волна,

x

Направление колебаний

Точек среды

N_t

2. Поперечные – частицы среды совершают колебания перпендикулярно направлению распространения волны – на поверхности жидкости.

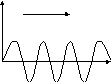x

Волна

T

Основные понятия (характеристики волны).

1. Скорость- 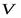- расстояние, которое проходит волна за единицу времени (1 сек.). В однородной среде скорость постоянна. Скорость зависит от свойств среды – упругости и плотности (чем больше плотность и упругость среды, тем больше скорость волны). Скорость в твёрдых телах выше скорости в жидких средах, а в жидких средах – выше, чем в газах. Скорость волны – отношение длины волны к периоду: .

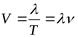2. Длина волны- 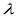- расстояние, которое прошла волна за время, равное периоду колебаний – расстояние между 2 точками, фазы которых в один и тот же момент времени отличаются на 2 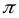. Единица измерения длины волны – метры.

3. Фронт волны– геометрическое место точек, колеблющихся в одинаковой фазе.

4. Уравнение волны– зависимость смещения колеблющейся точки, участвующей в волновом процессе, от координаты её равновесного положения и времени: .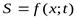

y

Б

T₁ t₂

А б` x

Х

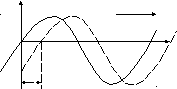
Пусть а колеблется по закону: .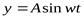

Тогда в колеблется с запаздыванием на угол 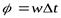, где 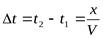, т.е.

.

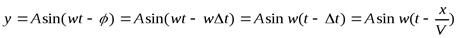5. Энергия волны.

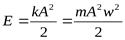- полная энергия одной частицы. Если частицn, то 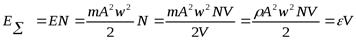, где 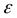- эпсилон,v– объём.

Эпсилон – энергия в единице объёма волны – объёмная плотность энергии.

Поток энергии волн равен отношению энергии, переносимой волнами через некоторую поверхность, к времени, в течение которого этот перенос осуществлён: 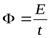, ватт; 1 ватт = 1дж/с.

6. Плотность потока энергии – интенсивность волны– поток энергии через единицу площади - величина, равная средней энергии, переносимой волной в единицу времени за единицу площади поперечного сечения.

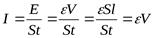[вт/м²]

.

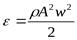Механические волны.

Механическая волна– механические возмущения, распространяющиеся в пространстве и несущие энергию.

Виды механических волн:

1. Упругие волны – распространение упругих деформаций;

2. Волны на поверхности жидкости.

Уравнение плоской волны, распространяющейся вдоль оси х.

Уравнение плоской волны, распространяющейся в произвольном направлении.

Найдем уравнение плоской волны, распространяющейся в направлении, образующем с осями координат х, у, z углы 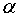, 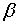и 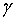. Пусть колебания в плоскости, проходящей через начало координат (рис. 196), имеют вид

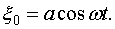
(79.1)

Возьмем волновую поверхность (плоскость)» отстоящую от начала координат на расстоянии l. Колебания в этой плоскости будут отставать от колебаний (79.1) на время ;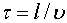

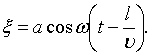
(79.2)

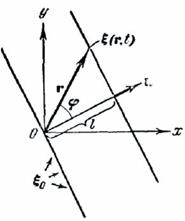
Рис. 196.

Выразим lчерез радиус-вектор r точек рассматриваемой поверхности. Для этого введем единичный вектор n нормали к волновой поверхности. Легко видеть, что скалярное произведение n на радиус-вектор r любой из точек поверхности имеет одно и то же значение, равное l;

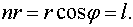
(79.3)

Подставим выражение (79.3) для l в уравнение (79.2), внеся одновременно в скобки :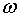

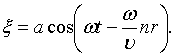
(79.4)

Отношение 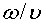равно волновому числу k[см. (787)]. Вектор

Равный по модулю волновому числу 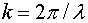и имеющий направление нормали к волновой поверхности, называется волновым вектором. Введя k в (79.4), получим:

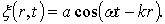
(79.6)

Функция (79.6) дает отклонение от положения равновесия точки с радиусом-вектором r[1] в момент времени t.

Чтобы перейти от радиуса-вектора точки к ее координатам х, у, z, выразим скалярное произведение kr через проекции векторов на координатные оси

Kr=k_xx+k_yy+k_zz.

Тогда уравнение плоской волны принимает вид

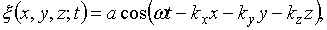
(79.7)

Где 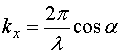, , 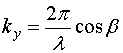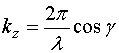. Функция (79.7) дает отклонение точки с координатами х, у, z в момент времени t. В случае, когда n совпадает с осью х, k_x=k, k_y=k_z=0, и уравнение (79.7) переходит в уравнение (78.8).

Уравнение плоской волны иногда пишут в виде

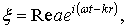
(79.8)

Причем часто опускают знак re и пишут просто

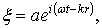
(79.9)

Подразумевая, что берется только вещественная часть этого выражения.

Уравнение сферической волны.

В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.

Предположим, что фаза колебаний источника равна wt (т.е. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону.

Энергия механических волн, поток энергии, плотность потока энергии. Вектор Умова. Количество энергии, переносимой волной за единицу времени через некоторую поверхность называют потоком энергии.

Ф=dw/dt

1дж/1c=1вт

Количество энергии, переносимое волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространению волны, называют плотностью потока энергии

J = dф/(dt*s)

1вт на 1кв м

Плотность потока энергии волны

J=ecp*v

Вектор умова - вектор плотности потока энергии физического поля; численно равен энергии, переносимой в единицу времени через единичную площадку, перпендикулярную направлению потока энергии в данной точке.

(рисунок не нашла,он на странице учебника 33)

Среднюю энергию ,переносимою волной за ед времени через ед площадку,перпендикулярно направлению распространения волны, называют интенсивностью волны.

I=w(cp)/(t*s)