Сечения методом Мора-Максвелла

Метод начальных параметров целесообразно использовать для построения эпюр прогибов и углов поворота сечений балки. При необходимости определения прогиба или угла поворота одного сечения балки, то лучше использовать интеграл Мора-Максвелла, или правило Верещагина.

Согласно методу Мора-Максвелла, для определения перемещения какого-либо сечения балки нужно образовать два состояния балки. Первое состояние называемое действительным, в котором балка нагружена рабочими силами (это состояние будем обозначать индексом F). Второе это возможное или единичное состояние, в котором балка нагружается лишь одной сосредоточенной нагрузкой (силой или моментом) равной единицы(это состояние будем обозначать буквой i).

Характер и направление действия нагрузки единичного состояния зависит от характера и направления перемещения, которое определяется. Если определяется вертикальное перемещение (прогиб балки в какой-нибудь точке её оси), то возможное состояние балки образуется путем нагружения балки в этой точке единичной вертикальной сосредоточенной силой F_i=1. На рис.11.24,а представлена балка в действительном состоянии, а на рис.11.24,б – балка в возможном (единичном) состоянии, созданном для определения вертикального перемещения Δ_iF действительного состояния.

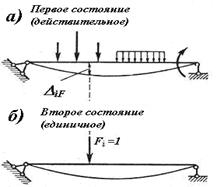
Рис.11.24

Если определяется угол поворота какого-либо сечения балки, то возможное состояние балки образуется путем нагружения балки в этом сечении единичным сосредоточенным моментом М_i=1 (рис.11.256).

Перемещение балки, вне зависимости от его характера, будем обозначать через Δ_iF – где первый индекс указывает направление перемещения, а второй соответствует нагрузке, от действия которой оно возникает. Индексы можно принимать цифровыми вместо буквенных (например, перемещение Δ₁₂ - есть перемещение в направлении действия силы F₁=1 от действия какой-нибудь силы F₂).

При определении перемещений балки при поперечном изгибе учитывается действие только изгибающих моментов и не учитывается действие поперечных сил, влияние которых на перемещение значительно меньше от влияния изгибающих моментов. Тогда формула Мора-Максвелла для определения перемещений, будет иметь вид:

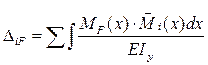(11.58)

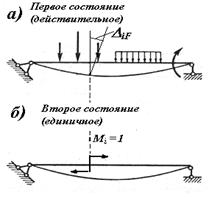
Рис.11.25

Таким образом, перемещение какого-либо сечения балки определяется суммой интегралов от произведения изгибающих моментов в двух состояниях балки деленной на жесткость балки при изгибе.

Формула Мора-Максвелла содержит уравнение изгибающих моментов на каждом участке двух состояний балки:

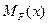- уравнение изгибающих моментов на некотором участке действительного состояния балки, которая загружена заданными внешними силами;

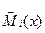- уравнение изгибающих моментов на том же участке возможного состояния балки, которая загружена одной сосредоточенной силой F_i=1, или одним сосредоточенным моментом М_i=1 в зависимости от того, какой вид перемещения определятся. Уравнение изгибающих моментов в единичном состоянии обозначается символом момента с черточкой над ним ;

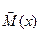ЕI_y – есть жесткость балки при изгибе на участке, который рассматривается.

Интегрирование произведения изгибающих моментов осуществляется в пределах каждого участка, а затем находится сумма полученных результатов.

Примечание: действительное состояние балки может иметь простое загружение в виде одной сосредоточенной силы F=1, или одного сосредоточенного момента М=1. В этом случае перемещения произвольного сечения балки называют единичными и обозначают символом δ_iF. Единичные перемещения определяются с использованием следующей формулы:

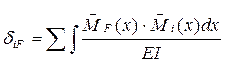(11.59)