Напряжения в наклоненных сечениях стержня
Рассмотрим стержень, на который действует сила растяжения F (рис. 9.6,а). Через произвольную точку nпроведем поперечное сечение nn2,площадь которого равняется A и сечение nn1, расположенное под углом α относительно поперечного сечения. Площадь этого сечения обозначим через Aα.
Соотношение между площадями двух сечений определяется равенством:
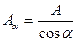 (9.3)
(9.3)
В точках наклоненного сечения nn1действуют равномерно распределенные напряжения p(рис.9.6,б). Равнодействующая этих напряжений равняется произведению pAαи направлена вдоль оси стержня. Из условия равновесия нижней части стержня имеем: ΣXi =0, pAα - F = 0, откуда pAα = F, или
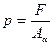 (9.4)
(9.4)
Подставим в зависимость (9.4) вместо площади Aα ее значения из зависимости (9.3), в результате получим:
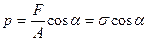 , окончательно
, окончательно 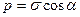 (9.5)
(9.5)
Пользуясь правилом параллелограмма, разложим напряжение pна две составляющие: σαи τα. Составляющая σα направлена перпендикулярно наклоненному сечению и называется нормальным напряжением в наклонном сечении, а составляющая τα действует в плоскости сечения и называется касательным напряжением в том же сечении (рис. 9.6,в). Нормальное напряжение в наклоненном сечении стержня имеет положительный знак в случае, если оно направлено от сечения (напряжение растяжения) и отрицательный знак, если оно направлено к сечению (напряжение сжатия).
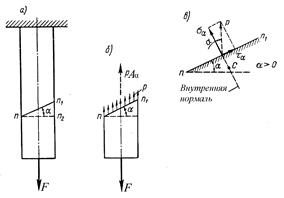
Рис.9.6
Касательное напряжениеτα в наклоненном сечении принимается положительным, если вектор этого напряжения пытается повернуть отсеченную часть стержня в направлении часовой стрелки относительно произвольной точки С, расположенной на внутренней нормали сечения.
Из силового треугольника (рис 9.6,в), находим:
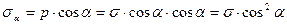 , или
, или
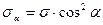 (9.6)
(9.6)
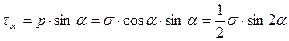 , или
, или
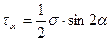 (9.7)
(9.7)
Анализируя формулы (9.6) и (9.7), можем сделать следующие выводы:
1) Нормальные напряжения имеют максимальные значения при α = 0 (т.е. в поперечных сечениях стержня) и нулевые значения при α = 900 (т.е. в сечениях параллельных оси стержня).
2) Касательные напряжения имеют максимальные значения в сечениях, расположенных под углом 450 к оси стержня. Из формулы (9.7), при α = 450, легко найдем максимальное значение касательного напряжения, равное половине нормального напряжения, которое возникает в поперечном сечении стержня. При α = 900 по той же формуле находим τα = 0.Таким образом, в сечениях стержня, параллельных оси, касательные напряжения не возникают.
Дата добавления: 2018-11-26; просмотров: 1017;











