Радиусы инерции. Эллипс инерции.

Рассмотрим плоское сечение бруса произвольной формы относительно произвольной системы координат y0z. Момент инерции этого сечения относительно оси yбудет определяться интегралом:

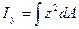
Обозначим среднее значение интеграла через 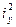и используем теорему о среднем значении интеграла. В результате получим:

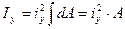, откуда 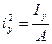,или

(8.31)

аналогично 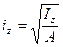(8.32)

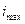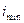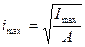Величины i_yи i_zявляются радиусами инерции сечения относительно соответствующих осей координат. Радиусы инерции сечения относительно главных центральных осей являются главными радиусами инерции. Они имеют экстремальные значения и .

и 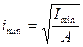(8.33)

Радиус инерции является удобной геометрической характеристикой плоского сечения. С его помощью можно геометрически исследовать изменение моментов инерции в зависимости от положения осей, то есть от их поворота. Для этого нужно определить 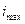и 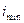и построить эллипс инерции на главных осях. Положим, что ось максимальной инерции u расположена горизонтально, а ось минимальной инерции сечения – вертикально.

Отложим от центра сечения в двух направлениях отрезок 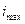перпендикулярно оси максимальной инерции u. Получим большую ось эллипса. Потом отложим отрезок 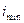перпендикулярно оси минимальной инерцииvв двух направлениях и получим малую ось эллипса.

Построим эллипс, пользуясь правилами начертательной геометрии (рис. 8.10) и покажем, как при его использовании определяется момент инерции относительно произвольной оси y, проведенной под углом α оси u. Проведем касательную к эллипсу параллельно осе y. Она пройдет через точку Д эллипса. Опустим из центра О перпендикуляр ОС к этой касательной. Отрезок ОС есть радиус инерции 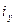в масштабе чертежа, тогда 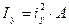_. Аналогично определяются моменты инерции сечения относительно произвольной оси.

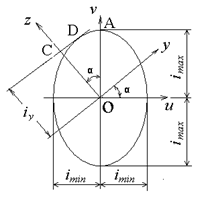
Рис. 8.10