Статическим моментом площади сечения относительно произвольной оси называется интеграл произведения элементарной части dA этой площади на ее расстояние от оси.
Статический момент измеряется в единицах длины, возведенных в третью степени (см3, м3).
Рассмотрим плоскую фигуру произвольной формы (рис.8.2).

Рис. 8.2
Проведем через произвольную точку плоскости горизонтальную ось y, и вертикальную ось z. Выделим элементарную часть dAплощади фигуры, координаты которой соответственно равняются y и z. Заметим, что всякая площадь может рассматриваться как сумма безгранично большого количества элементарных частей dA. Тогда статические моменты площади заданной фигуры относительно осей yи zбудут определяться соответственно следующими интегралами:
 (8.1)
(8.1)
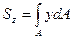 (8.2)
(8.2)
Проведем затем через центр тяжести сечения Осцентральные оси yси zс параллельно осям y и zи вычислим статические моменты относительно центральных осей, если известны статические моменты относительно произвольных осей yи z. Координаты элементарной части dAплощади сечения относительно этих осей соответственно равны y – yси z – zс(смотри рис.8.2), тогда:
 (8.3)
(8.3)
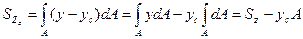 (8.4)
(8.4)
Из теоретической механики известно, что статические моменты относительно центральных осей всегда равны нулю, то есть 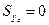 ;
; 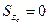 , тогда
, тогда
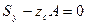 , откуда
, откуда 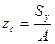 (8.5)
(8.5)
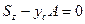 , откуда
, откуда 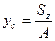 (8.6)
(8.6)
Эти формулы используют для определения координат центра тяжести плоской фигуры произвольной формы, и произвольных размеров.
Если плоская фигура составлена из нескольких частей простой формы, площади которых и положения центров тяжести известны, то статический момент определяется как сумма статических моментов отдельных фигур, то есть:
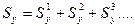 ==
== 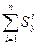 (8.7)
(8.7)
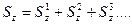 ==
== 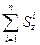 (8.8)
(8.8)
Координаты центра тяжести сложной фигуры (плоского сечения бруса) определяются по формулам (8.5) и (8.6) соответственно.
Пример 8.1: Определить координаты центра тяжести плоского сечения, составленного из прямоугольника размерами h = 1 см, b = 24 см, и двутавра №16
(рис. 8.3).
Решение: Из таблиц сортамента прокатной стали, находим размеры двутавра и его площадь: H = 16 см, B = 8.1 см, А1 = 20,2 см2 (приложение 2). Определяем площадь прямоугольника А2 = 1. 24 = 24 см2.
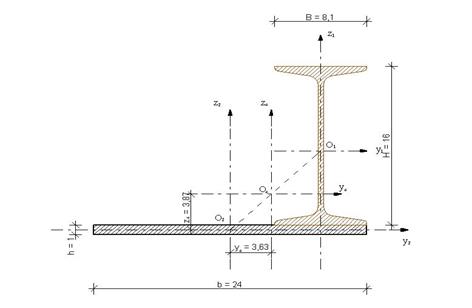
Рис. 8.3
На чертеже сечения проведем собственные центральные оси отдельных его частей через их центры тяжести (оси y1и z1через центр О1 двутавра и оси y2и z2через центр О2 прямоугольника). Определим статические моменты всего сечения относительно осей y2и z2. Вспомогательные оси координат целесообразно выбрать так, чтобы координаты центров тяжести отдельных частей сечения были положительными, или равными нулю.
Учитывая размеры и расположения отдельных частей сечения, определяем координаты их центров тяжести относительно осей y2и z2.В этом случае координаты точки О1 будут иметь положительные знаки: y1=b/2- B/2 = 24/2 - 8,1/2 = 7,95 см;
z1=h/2+ H/2 = 1/2 + 16/2 = 8,5 см. Координаты точки О2 будут иметь нулевые значения:
y2 = 0; z2 = 0.
Определяем статические моменты сечения относительно осей y2и z2, используя формулы (2.7 ) и (2.8).
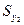 =
= 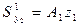 = 20,2 . 8,5 = 171,7 см3
= 20,2 . 8,5 = 171,7 см3
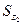 =
= 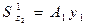 = 20,2 . 7,95 = 160,59 см3
= 20,2 . 7,95 = 160,59 см3
Определяем координаты центра тяжести всего сечения по формулам (2.5) и (2.6):
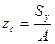 = 171,1/(20,2+24)= 3,87 см,
= 171,1/(20,2+24)= 3,87 см,
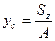 = 160,59/(20,2+24)= 3,63 см.
= 160,59/(20,2+24)= 3,63 см.
Таким образом, центр тяжести сечения находится на расстоянии 3,87 см от оси y2и на расстоянии 3,63 см от оси z2(рис. 8.3). Следует иметь в виду, что центр тяжести сечения, составленного из двух фигур, всегда находится на линии, которая соединяет центры тяжести составляющих фигур. Это свойство используют для проверки решения задачи.
Дата добавления: 2018-11-26; просмотров: 1188;











