Закон распределения Нернста. Экстракция

Если взять две несмешивающиеся жидкости и добавить третий компонент, то он будет растворяться в разной степени в том и другом растворителе. При установлении равновесия отношение концентраций полученных растворов будет постоянным при данной температуре

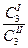= К, это выражение закона распределения Нернста, где

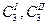- концентрации третьего компонента в I и II фазах;

К - коэффициент распределения.

Если растворенное вещество диссоциирует или ассоциирует в одном из растворителей, то уравнение Нернста имеет вид:

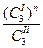= К

Для нахождения Кип логарифмируем уравнение и получаем уравнение прямой

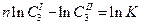
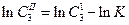
Построив прямую в координатах 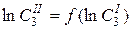, найдем «п» как тангенс угла наклона прямой (по любым двум точкам, лежащим на прямой) tga =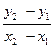

InK можно найти из уравнения , подставив в него значения любой точки, находящейся на прямой.

Этот закон лежит в основе процесса экстракции. Экстракция это извлечение компонента из одной фазы в другую. Экстракция бывает твердофазная - извлечение веществ из твердой фазы в жидкую (например, заваривание чая, кофе, приготовление настоек, экстрактов трав и т.д.) и жидкофазная - извлечение растворенного вещества из жидкого раствора экстрагентом. Раствор извлеченного вещества в экстрагенте называется экстрактом, а исходный раствор после извлечения из него вещества называется рафинатом.

Для расчета эффективности жидкофазной экстракции используют уравнение

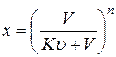(3.31)

Где х - доля неизвлеченного вещества в рафинате;

V - объем исходного раствора;

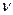- объем экстрагента;

К - коэффициент распределения

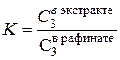
п - число экстракций.

Как видно из уравнения, чем больше экстракций, тем меньше остается вещества в рафинате, то есть неизвлеченным, тем больше вещества извлекается экстрагентом. Эффективность экстракции в большой степени определяется величиной коэффициента распределения: чем больше коэффициент в пользу экстрагента, тем эффективнее экстракция.

Часто в справочнике дается коэффициент распределения как отношение концентраций в рафинате к экстракту, то есть величина, обратная той, что должна быть в уравнении (). В этом случае следует взять величину обратную справочной и использовать в уравнении ().